
Question Number 165641 by nadovic last updated on 05/Feb/22
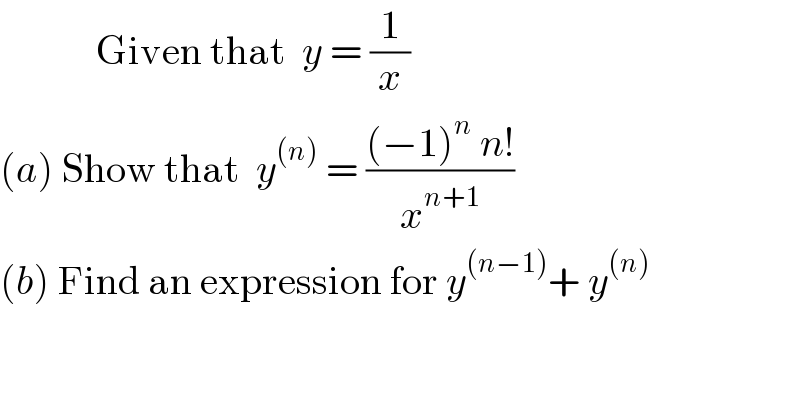
$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{Given}\:\mathrm{that}\:\:{y}\:=\:\frac{\mathrm{1}}{{x}}\: \\ $$$$\left({a}\right)\:\mathrm{Show}\:\mathrm{that}\:\:{y}^{\left({n}\right)} \:=\:\frac{\left(−\mathrm{1}\right)^{{n}} \:{n}!}{{x}^{{n}+\mathrm{1}} } \\ $$$$\left({b}\right)\:\mathrm{Find}\:\mathrm{an}\:\mathrm{expression}\:\mathrm{for}\:{y}^{\left({n}−\mathrm{1}\right)} +\:{y}^{\left({n}\right)} \\ $$$$ \\ $$
Answered by aleks041103 last updated on 05/Feb/22
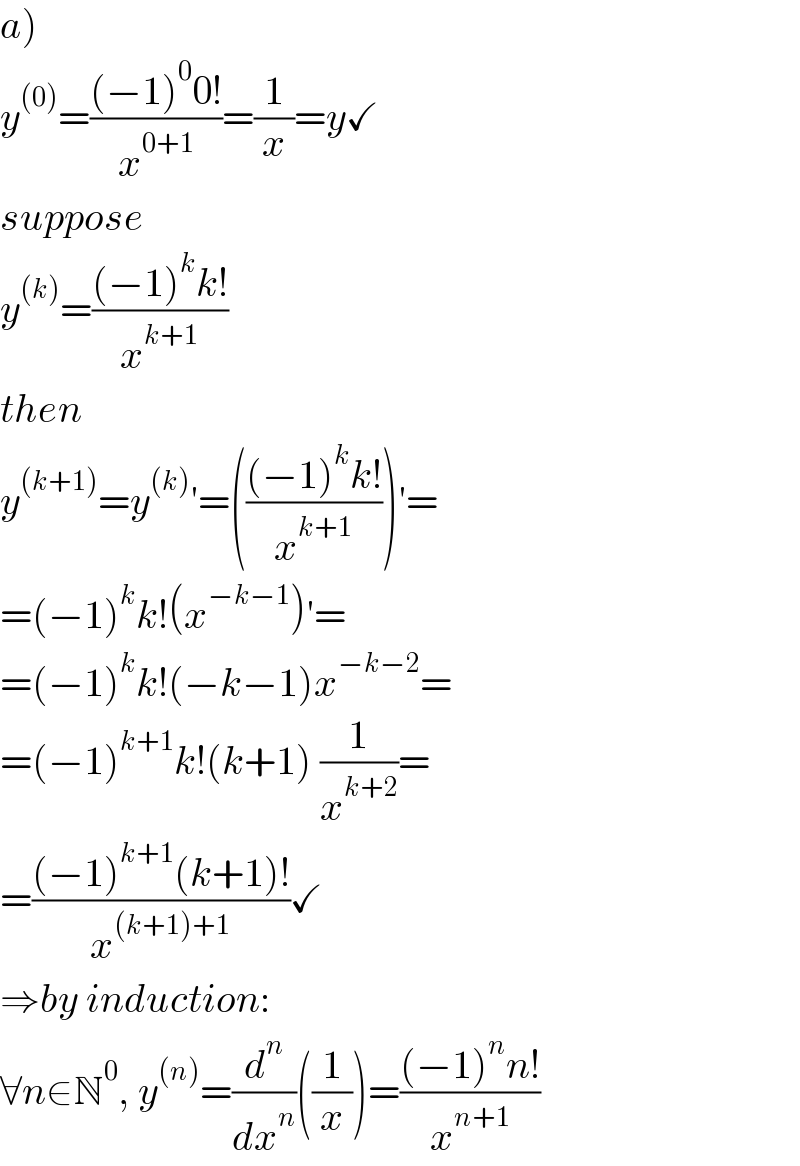
$$\left.{a}\right) \\ $$$${y}^{\left(\mathrm{0}\right)} =\frac{\left(−\mathrm{1}\right)^{\mathrm{0}} \mathrm{0}!}{{x}^{\mathrm{0}+\mathrm{1}} }=\frac{\mathrm{1}}{{x}}={y}\checkmark \\ $$$${suppose} \\ $$$${y}^{\left({k}\right)} =\frac{\left(−\mathrm{1}\right)^{{k}} {k}!}{{x}^{{k}+\mathrm{1}} } \\ $$$${then} \\ $$$${y}^{\left({k}+\mathrm{1}\right)} ={y}^{\left({k}\right)} '=\left(\frac{\left(−\mathrm{1}\right)^{{k}} {k}!}{{x}^{{k}+\mathrm{1}} }\right)'= \\ $$$$=\left(−\mathrm{1}\right)^{{k}} {k}!\left({x}^{−{k}−\mathrm{1}} \right)'= \\ $$$$=\left(−\mathrm{1}\right)^{{k}} {k}!\left(−{k}−\mathrm{1}\right){x}^{−{k}−\mathrm{2}} = \\ $$$$=\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} {k}!\left({k}+\mathrm{1}\right)\:\frac{\mathrm{1}}{{x}^{{k}+\mathrm{2}} }= \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \left({k}+\mathrm{1}\right)!}{{x}^{\left({k}+\mathrm{1}\right)+\mathrm{1}} }\checkmark \\ $$$$\Rightarrow{by}\:{induction}: \\ $$$$\forall{n}\in\mathbb{N}^{\mathrm{0}} ,\:{y}^{\left({n}\right)} =\frac{{d}^{{n}} }{{dx}^{{n}} }\left(\frac{\mathrm{1}}{{x}}\right)=\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{{x}^{{n}+\mathrm{1}} } \\ $$
Answered by aleks041103 last updated on 05/Feb/22
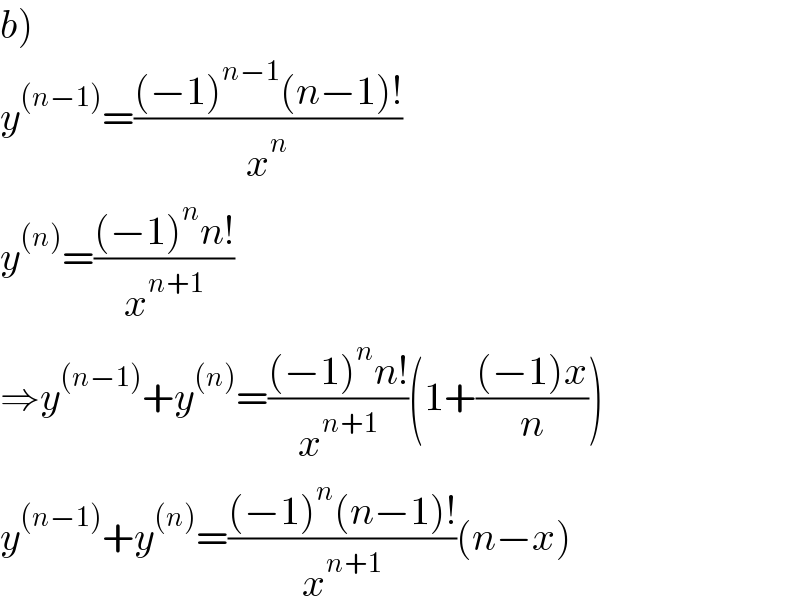
$$\left.{b}\right) \\ $$$${y}^{\left({n}−\mathrm{1}\right)} =\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{{x}^{{n}} } \\ $$$${y}^{\left({n}\right)} =\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{{x}^{{n}+\mathrm{1}} } \\ $$$$\Rightarrow{y}^{\left({n}−\mathrm{1}\right)} +{y}^{\left({n}\right)} =\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{{x}^{{n}+\mathrm{1}} }\left(\mathrm{1}+\frac{\left(−\mathrm{1}\right){x}}{{n}}\right) \\ $$$${y}^{\left({n}−\mathrm{1}\right)} +{y}^{\left({n}\right)} =\frac{\left(−\mathrm{1}\right)^{{n}} \left({n}−\mathrm{1}\right)!}{{x}^{{n}+\mathrm{1}} }\left({n}−{x}\right) \\ $$
