
Question Number 165218 by Lordose last updated on 27/Jan/22
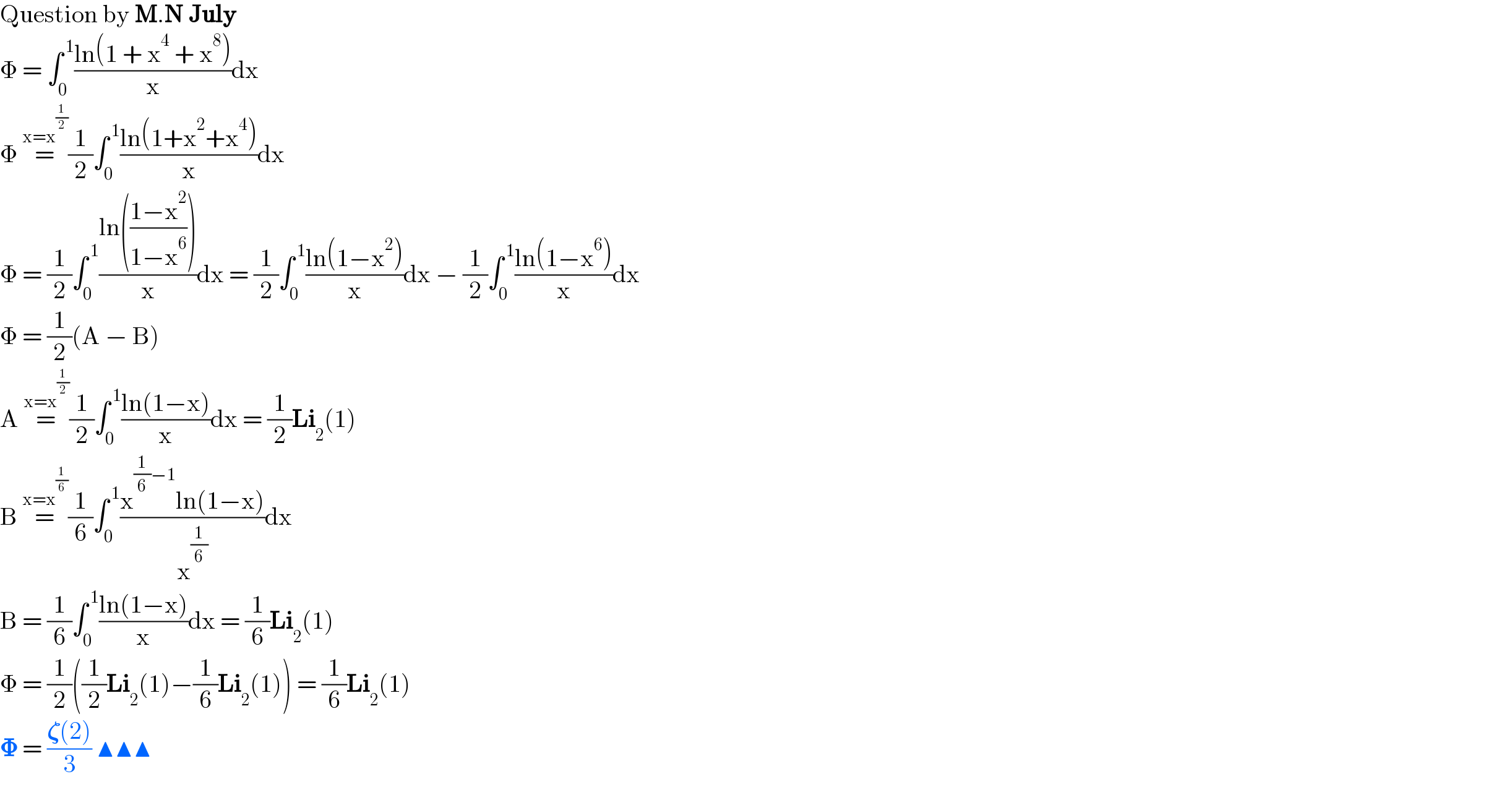
$$\mathrm{Question}\:\mathrm{by}\:\boldsymbol{\mathrm{M}}.\boldsymbol{\mathrm{N}}\:\boldsymbol{\mathrm{July}} \\ $$$$\Phi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}\:+\:\mathrm{x}^{\mathrm{4}} \:+\:\mathrm{x}^{\mathrm{8}} \right)}{\mathrm{x}}\mathrm{dx} \\ $$$$\Phi\:\overset{\mathrm{x}=\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} } {=}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{4}} \right)}{\mathrm{x}}\mathrm{dx} \\ $$$$\Phi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{x}^{\mathrm{6}} }\right)}{\mathrm{x}}\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}}\mathrm{dx}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{6}} \right)}{\mathrm{x}}\mathrm{dx} \\ $$$$\Phi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}\:−\:\mathrm{B}\right) \\ $$$$\mathrm{A}\:\overset{\mathrm{x}=\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} } {=}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{Li}}_{\mathrm{2}} \left(\mathrm{1}\right) \\ $$$$\mathrm{B}\:\overset{\mathrm{x}=\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{6}}} } {=}\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} \mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{6}}} }\mathrm{dx} \\ $$$$\mathrm{B}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\boldsymbol{\mathrm{Li}}_{\mathrm{2}} \left(\mathrm{1}\right)\: \\ $$$$\Phi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{Li}}_{\mathrm{2}} \left(\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{6}}\boldsymbol{\mathrm{Li}}_{\mathrm{2}} \left(\mathrm{1}\right)\right)\:=\:\frac{\mathrm{1}}{\mathrm{6}}\boldsymbol{\mathrm{Li}}_{\mathrm{2}} \left(\mathrm{1}\right) \\ $$$$\boldsymbol{\Phi}\:=\:\frac{\boldsymbol{\zeta}\left(\mathrm{2}\right)}{\mathrm{3}}\:\blacktriangle\blacktriangle\blacktriangle \\ $$
Commented by mnjuly1970 last updated on 27/Jan/22
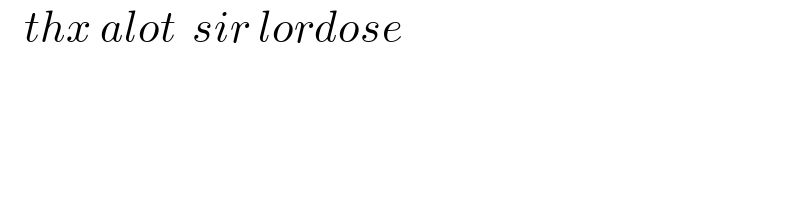
$$\:\:\:{thx}\:{alot}\:\:{sir}\:{lordose} \\ $$
Answered by Ar Brandon last updated on 27/Jan/22
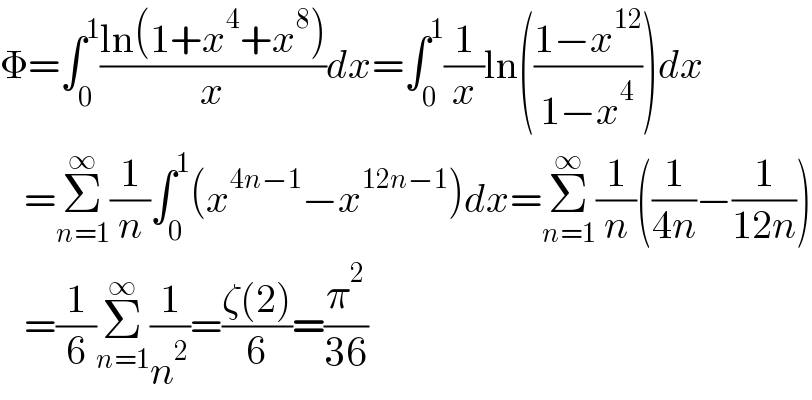
$$\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}^{\mathrm{4}} +{x}^{\mathrm{8}} \right)}{{x}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}}\mathrm{ln}\left(\frac{\mathrm{1}−{x}^{\mathrm{12}} }{\mathrm{1}−{x}^{\mathrm{4}} }\right){dx} \\ $$$$\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{\mathrm{4}{n}−\mathrm{1}} −{x}^{\mathrm{12}{n}−\mathrm{1}} \right){dx}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\left(\frac{\mathrm{1}}{\mathrm{4}{n}}−\frac{\mathrm{1}}{\mathrm{12}{n}}\right) \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{6}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{6}}=\frac{\pi^{\mathrm{2}} }{\mathrm{36}} \\ $$
Commented by amin96 last updated on 28/Jan/22

$$\boldsymbol{\mathrm{correct}}\:\boldsymbol{\mathrm{sir}}.\:\boldsymbol{\mathrm{great}}\:\boldsymbol{\mathrm{solution}} \\ $$
