
Question Number 163736 by HongKing last updated on 09/Jan/22
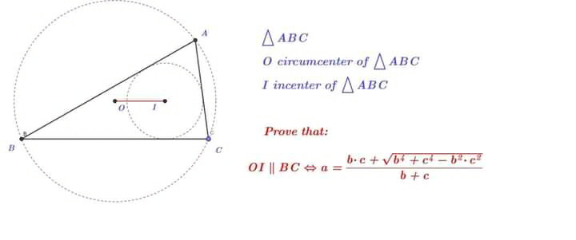
Answered by mr W last updated on 10/Jan/22
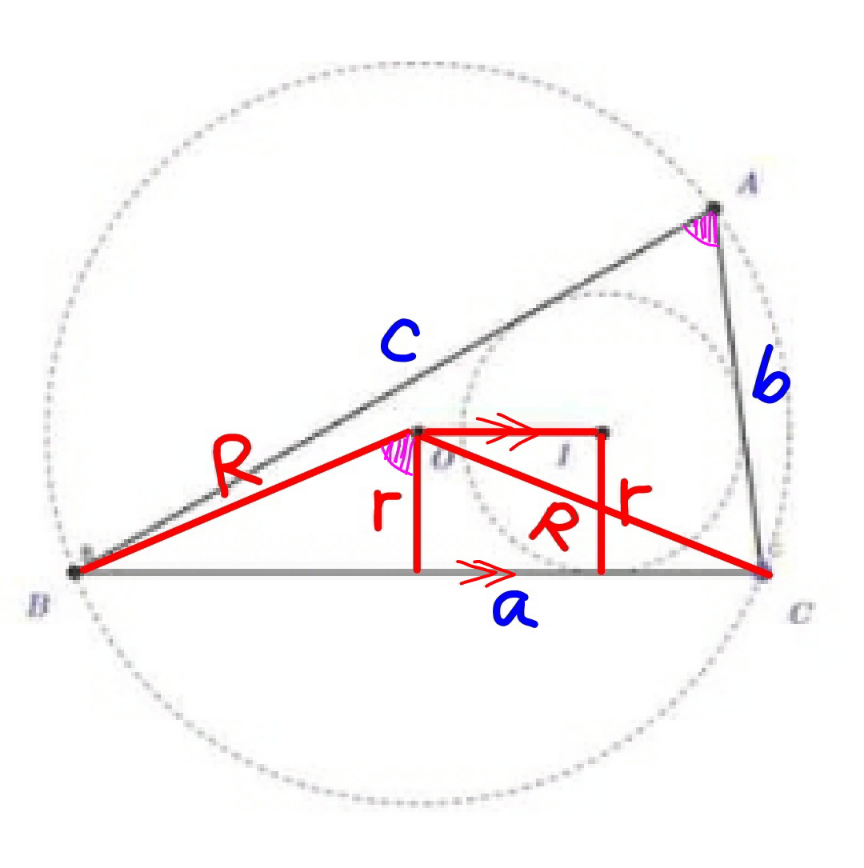
Commented by mr W last updated on 10/Jan/22
![R=(a/(2 sin A)) Δ=((bc sin A)/2) r=((2Δ)/(a+b+c))=((bc sin A)/(a+b+c)) OI//AB ⇔ R cos A=r (a/(2 sin A)) cos A=((bc sin A)/(a+b+c)) cos A=((2bc sin^2 A)/(a(a+b+c))) cos A=((2bc(1−cos A)(1+cos A))/(a(a+b+c))) ((b^2 +c^2 −a^2 )/(2bc))=((2bc(1−((b^2 +c^2 −a^2 )/(2bc)))(1+((b^2 +c^2 −a^2 )/(2bc))))/(a(a+b+c))) b^2 +c^2 −a^2 =(([a^2 −(b−c)^2 ][(b+c)^2 −a^2 ])/(a(a+b+c))) b^2 +c^2 −a^2 =(([a^2 −(b−c)^2 ](b+c−a))/a) (b+c)a^2 −2bca−(b^2 −c^2 )(b−c)=0 a=((bc+(√(b^2 c^2 +(b+c)(b^2 −c^2 )(b−c))))/(b+c)) a=((bc+(√(b^2 c^2 +(b^2 −c^2 )^2 )))/(b+c)) ⇒a=((bc+(√(b^4 +c^4 −b^2 c^2 )))/(b+c)) ✓](Q163774.png)
$${R}=\frac{{a}}{\mathrm{2}\:\mathrm{sin}\:{A}} \\ $$$$\Delta=\frac{{bc}\:\mathrm{sin}\:{A}}{\mathrm{2}} \\ $$$${r}=\frac{\mathrm{2}\Delta}{{a}+{b}+{c}}=\frac{{bc}\:\mathrm{sin}\:{A}}{{a}+{b}+{c}} \\ $$$$\boldsymbol{{OI}}//\boldsymbol{{AB}}\:\Leftrightarrow\:\boldsymbol{{R}}\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{{A}}=\boldsymbol{{r}} \\ $$$$\frac{{a}}{\mathrm{2}\:\mathrm{sin}\:{A}}\:\mathrm{cos}\:{A}=\frac{{bc}\:\mathrm{sin}\:{A}}{{a}+{b}+{c}} \\ $$$$\mathrm{cos}\:{A}=\frac{\mathrm{2}{bc}\:\mathrm{sin}^{\mathrm{2}} \:{A}}{{a}\left({a}+{b}+{c}\right)} \\ $$$$\mathrm{cos}\:{A}=\frac{\mathrm{2}{bc}\left(\mathrm{1}−\mathrm{cos}\:{A}\right)\left(\mathrm{1}+\mathrm{cos}\:{A}\right)}{{a}\left({a}+{b}+{c}\right)} \\ $$$$\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}=\frac{\mathrm{2}{bc}\left(\mathrm{1}−\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}\right)\left(\mathrm{1}+\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}\right)}{{a}\left({a}+{b}+{c}\right)} \\ $$$${b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} =\frac{\left[{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} \right]\left[\left({b}+{c}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \right]}{{a}\left({a}+{b}+{c}\right)} \\ $$$${b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} =\frac{\left[{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} \right]\left({b}+{c}−{a}\right)}{{a}} \\ $$$$\left({b}+{c}\right){a}^{\mathrm{2}} −\mathrm{2}{bca}−\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)\left({b}−{c}\right)=\mathrm{0} \\ $$$${a}=\frac{{bc}+\sqrt{{b}^{\mathrm{2}} {c}^{\mathrm{2}} +\left({b}+{c}\right)\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)\left({b}−{c}\right)}}{{b}+{c}} \\ $$$${a}=\frac{{bc}+\sqrt{{b}^{\mathrm{2}} {c}^{\mathrm{2}} +\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)^{\mathrm{2}} }}{{b}+{c}} \\ $$$$\Rightarrow{a}=\frac{{bc}+\sqrt{{b}^{\mathrm{4}} +{c}^{\mathrm{4}} −{b}^{\mathrm{2}} {c}^{\mathrm{2}} }}{{b}+{c}}\:\checkmark \\ $$
Commented by Tawa11 last updated on 10/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by HongKing last updated on 10/Jan/22
$$\mathrm{very}\:\mathrm{nice}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
