
Question Number 163452 by HongKing last updated on 07/Jan/22
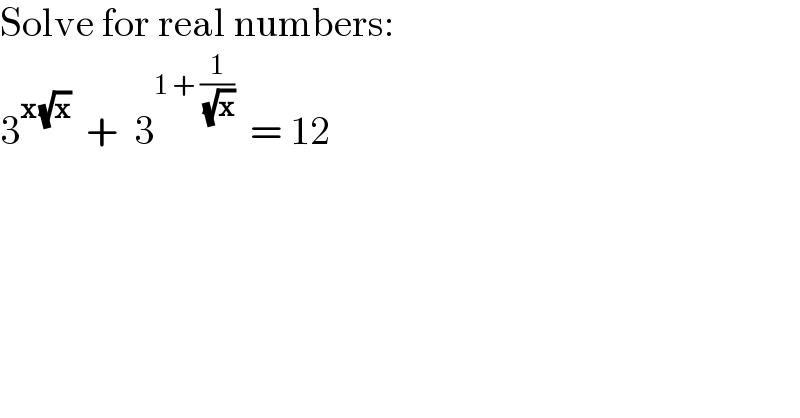
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\mathrm{3}^{\boldsymbol{\mathrm{x}}\:\sqrt{\boldsymbol{\mathrm{x}}}} \:\:+\:\:\mathrm{3}^{\mathrm{1}\:+\:\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{\mathrm{x}}}}} \:\:=\:\mathrm{12} \\ $$
Commented by mr W last updated on 07/Jan/22

$${i}\:{don}'{t}\:{think}\:{such}\:{equations}\:{have} \\ $$$${much}\:{technique}\:{values}.\:{basically} \\ $$$${we}\:{must}\:``{see}''\:{or}\:{guess}\:{the}\:{solutions}. \\ $$$${here}\:{for}\:{example}:\:{we}\:{guess}\:\mathrm{3}^{\mathrm{2}} +\mathrm{3}=\mathrm{12} \\ $$$${then}\:{see}\:{x}=\mathrm{1}\:{is}\:{ok}. \\ $$$${i}\:{say}\:{this}\:{has}\:{no}\:{technique}\:{value}, \\ $$$${but}\:{rather}\:{stupid},\:{because}\:{we}\:{are}\:{dead} \\ $$$${if}\:{the}\:{equation}\:{is} \\ $$$$\mathrm{3}^{\boldsymbol{\mathrm{x}}\:\sqrt{\boldsymbol{\mathrm{x}}}} \:\:+\:\:\mathrm{3}^{\mathrm{1}\:+\:\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{\mathrm{x}}}}} \:\:=\:\mathrm{11}. \\ $$$${i}\:{have}\:{never}\:{understood}\:{what}\:{the} \\ $$$${creators}\:\left({i}\:{don}'{t}\:{mean}\:{Hongking}\:{sir}\right) \\ $$$${of}\:{such}\:{questions}\:{want}\:{to}\:{test}\:{from} \\ $$$${the}\:{students}. \\ $$
Answered by mathlove last updated on 08/Jan/22
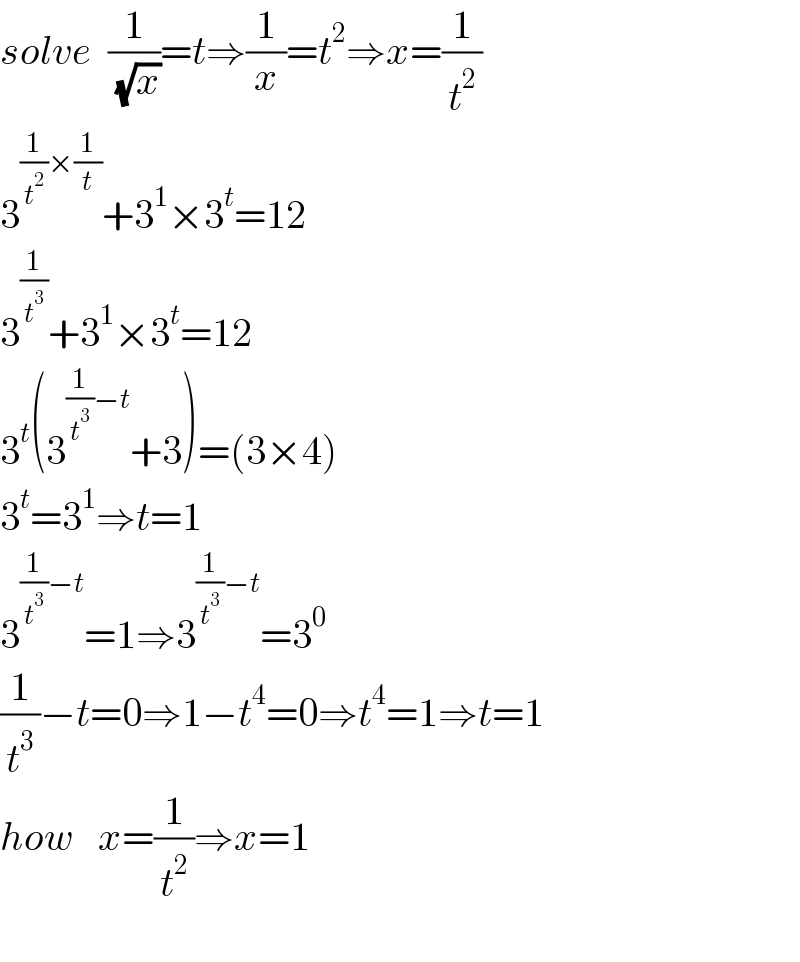
$${solve}\:\:\frac{\mathrm{1}}{\:\sqrt{{x}}}={t}\Rightarrow\frac{\mathrm{1}}{{x}}={t}^{\mathrm{2}} \Rightarrow{x}=\frac{\mathrm{1}}{{t}^{\mathrm{2}} } \\ $$$$\mathrm{3}^{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }×\frac{\mathrm{1}}{{t}}} +\mathrm{3}^{\mathrm{1}} ×\mathrm{3}^{{t}} =\mathrm{12} \\ $$$$\mathrm{3}^{\frac{\mathrm{1}}{{t}^{\mathrm{3}} }} +\mathrm{3}^{\mathrm{1}} ×\mathrm{3}^{{t}} =\mathrm{12} \\ $$$$\mathrm{3}^{{t}} \left(\mathrm{3}^{\frac{\mathrm{1}}{{t}^{\mathrm{3}} }−{t}} +\mathrm{3}\right)=\left(\mathrm{3}×\mathrm{4}\right) \\ $$$$\mathrm{3}^{{t}} =\mathrm{3}^{\mathrm{1}} \Rightarrow{t}=\mathrm{1} \\ $$$$\mathrm{3}^{\frac{\mathrm{1}}{{t}^{\mathrm{3}} }−{t}} =\mathrm{1}\Rightarrow\mathrm{3}^{\frac{\mathrm{1}}{{t}^{\mathrm{3}} }−{t}} =\mathrm{3}^{\mathrm{0}} \\ $$$$\frac{\mathrm{1}}{{t}^{\mathrm{3}} }−{t}=\mathrm{0}\Rightarrow\mathrm{1}−{t}^{\mathrm{4}} =\mathrm{0}\Rightarrow{t}^{\mathrm{4}} =\mathrm{1}\Rightarrow{t}=\mathrm{1} \\ $$$${how}\:\:\:{x}=\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\Rightarrow{x}=\mathrm{1} \\ $$$$ \\ $$
