
Question Number 163437 by cortano1 last updated on 07/Jan/22

Commented by mr W last updated on 07/Jan/22
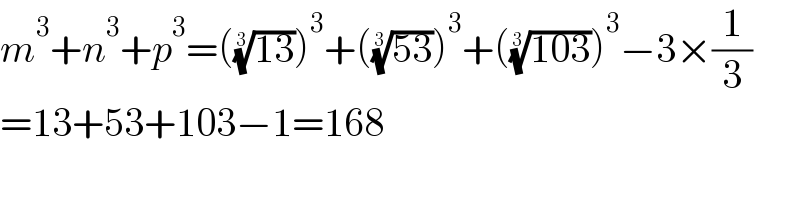
$${m}^{\mathrm{3}} +{n}^{\mathrm{3}} +{p}^{\mathrm{3}} =\left(\sqrt[{\mathrm{3}}]{\mathrm{13}}\right)^{\mathrm{3}} +\left(\sqrt[{\mathrm{3}}]{\mathrm{53}}\right)^{\mathrm{3}} +\left(\sqrt[{\mathrm{3}}]{\mathrm{103}}\right)^{\mathrm{3}} −\mathrm{3}×\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$=\mathrm{13}+\mathrm{53}+\mathrm{103}−\mathrm{1}=\mathrm{168} \\ $$
Commented by cortano1 last updated on 07/Jan/22
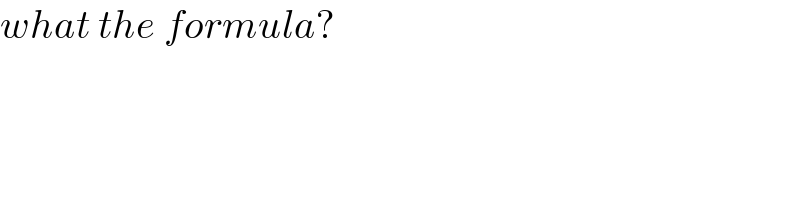
$${what}\:{the}\:{formula}? \\ $$
Answered by mr W last updated on 07/Jan/22

$${say}\:{m},{n},{p}\:{are}\:{the}\:{roots}\:{of}\:{eqn}. \\ $$$$\left({x}−\alpha\right)\left({x}−\beta\right)\left({x}−\gamma\right)=\delta,\:{i}.{e}. \\ $$$${x}^{\mathrm{3}} −\left(\alpha+\beta+\gamma\right){x}^{\mathrm{2}} +\left(\alpha\beta+\beta\gamma+\gamma\alpha\right){x}+\left(\alpha\beta\gamma−\delta\right)=\mathrm{0} \\ $$$${then}\:{we}\:{have} \\ $$$${m}+{n}+{p}=\alpha+\beta+\gamma \\ $$$${mn}+{np}+{pm}=\alpha\beta+\beta\gamma+\gamma\alpha \\ $$$${mnp}=\alpha\beta\gamma−\delta \\ $$$$\left({m}+{n}+{p}\right)^{\mathrm{2}} ={m}^{\mathrm{2}} +{n}^{\mathrm{2}} +{p}^{\mathrm{2}} +\mathrm{2}\left({mn}+{np}+{pm}\right) \\ $$$$\left(\alpha+\beta+\gamma\right)^{\mathrm{2}} =\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} +\mathrm{2}\left(\alpha\beta+\beta\gamma+\gamma\alpha\right) \\ $$$$\Rightarrow{m}^{\mathrm{2}} +{n}^{\mathrm{2}} +{p}^{\mathrm{2}} =\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \\ $$$$\Rightarrow\left({m}^{\mathrm{2}} +{n}^{\mathrm{2}} +{p}^{\mathrm{2}} \right)\left({m}+{n}+{p}\right)=\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)\left(\alpha+\alpha+\gamma\right) \\ $$$$\Rightarrow{m}^{\mathrm{3}} +{n}^{\mathrm{3}} +{p}^{\mathrm{3}} +\left({m}+{n}+{p}\right)\left({mn}+{np}+{pm}\right)−\mathrm{3}{mnp}=\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} +\beta^{\mathrm{3}} +\left(\alpha+\beta+\gamma\right)\left(\alpha\beta+\beta\gamma+\gamma\alpha\right)−\mathrm{3}\alpha\beta\gamma \\ $$$$\Rightarrow{m}^{\mathrm{3}} +{n}^{\mathrm{3}} +{p}^{\mathrm{3}} −\mathrm{3}{mnp}=\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} +\beta^{\mathrm{3}} −\mathrm{3}\alpha\beta\gamma \\ $$$$\Rightarrow{m}^{\mathrm{3}} +{n}^{\mathrm{3}} +{p}^{\mathrm{3}} −\mathrm{3}\left(\alpha\beta\gamma−\delta\right)=\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} +\beta^{\mathrm{3}} −\mathrm{3}\alpha\beta\gamma \\ $$$$\Rightarrow{m}^{\mathrm{3}} +{n}^{\mathrm{3}} +{p}^{\mathrm{3}} =\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} +\beta^{\mathrm{3}} −\mathrm{3}\delta \\ $$$${with}\:\alpha=\sqrt[{\mathrm{3}}]{\mathrm{13}},\:\beta=\sqrt[{\mathrm{3}}]{\mathrm{53}},\:\gamma=\sqrt[{\mathrm{3}}]{\mathrm{103}},\:\delta=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{m}^{\mathrm{3}} +{n}^{\mathrm{3}} +{p}^{\mathrm{3}} =\left(\sqrt[{\mathrm{3}}]{\mathrm{13}}\right)^{\mathrm{3}} +\left(\sqrt[{\mathrm{3}}]{\mathrm{53}}\right)^{\mathrm{3}} +\left(\sqrt[{\mathrm{3}}]{\mathrm{103}}\right)^{\mathrm{3}} \:−\mathrm{3}×\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{m}^{\mathrm{3}} +{n}^{\mathrm{3}} +{p}^{\mathrm{3}} =\mathrm{13}+\mathrm{53}+\mathrm{103}\:−\mathrm{1}=\mathrm{168}\:\blacksquare \\ $$
Commented by Tawa11 last updated on 07/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by cortano1 last updated on 07/Jan/22

$${very}\:{nice} \\ $$
Commented by peter frank last updated on 07/Jan/22

$$\mathrm{great} \\ $$
