
Question Number 163325 by mathlove last updated on 06/Jan/22
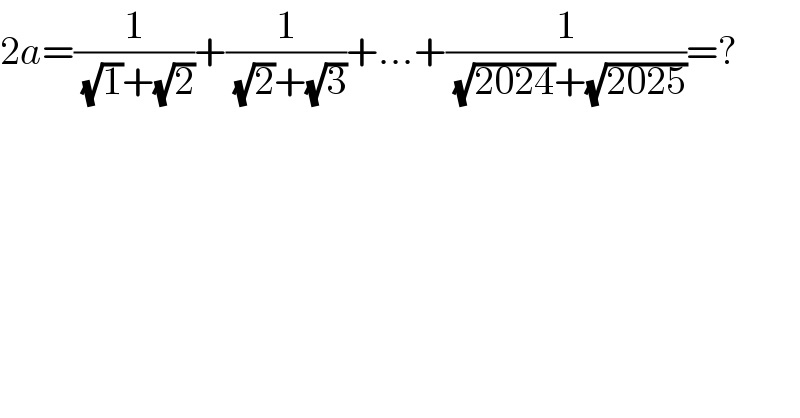
$$\mathrm{2}{a}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}}+\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}}+...+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2024}}+\sqrt{\mathrm{2025}}}=? \\ $$
Commented by cortano1 last updated on 06/Jan/22
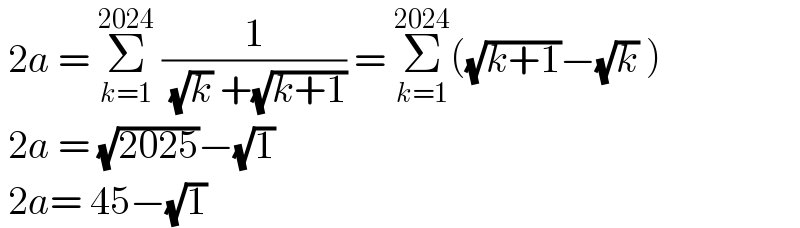
$$\:\mathrm{2}{a}\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{2024}} {\sum}}\:\frac{\mathrm{1}}{\:\sqrt{{k}}\:+\sqrt{{k}+\mathrm{1}}}\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{2024}} {\sum}}\left(\sqrt{{k}+\mathrm{1}}−\sqrt{{k}}\:\right) \\ $$$$\:\mathrm{2}{a}\:=\:\sqrt{\mathrm{2025}}−\sqrt{\mathrm{1}}\: \\ $$$$\:\mathrm{2}{a}=\:\mathrm{45}−\sqrt{\mathrm{1}} \\ $$
Commented by blackmamba last updated on 06/Jan/22

$${telescopic} \\ $$
Answered by mr W last updated on 06/Jan/22
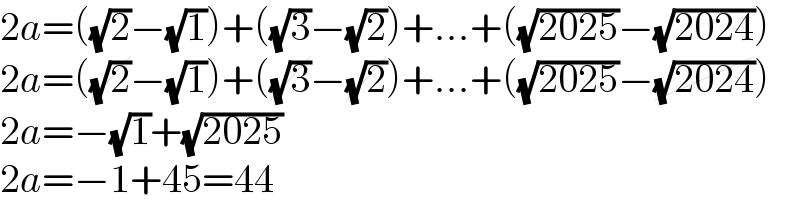
$$\mathrm{2}{a}=\left(\sqrt{\mathrm{2}}−\sqrt{\mathrm{1}}\right)+\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)+...+\left(\sqrt{\mathrm{2025}}−\sqrt{\mathrm{2024}}\right) \\ $$$$\mathrm{2}{a}=\left(\cancel{\sqrt{\mathrm{2}}}−\sqrt{\mathrm{1}}\right)+\left(\cancel{\sqrt{\mathrm{3}}}−\cancel{\sqrt{\mathrm{2}}}\right)+...+\left(\sqrt{\mathrm{2025}}−\cancel{\sqrt{\mathrm{2024}}}\right) \\ $$$$\mathrm{2}{a}=−\sqrt{\mathrm{1}}+\sqrt{\mathrm{2025}} \\ $$$$\mathrm{2}{a}=−\mathrm{1}+\mathrm{45}=\mathrm{44} \\ $$
