
Question Number 162864 by mathacek last updated on 01/Jan/22
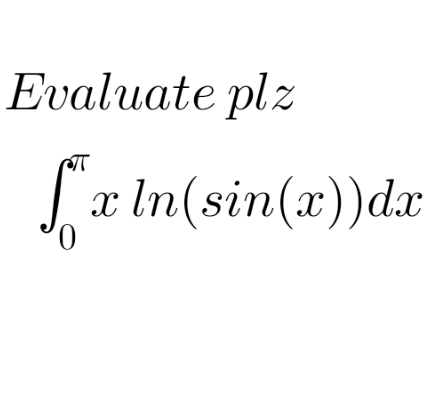
Answered by Ar Brandon last updated on 01/Jan/22
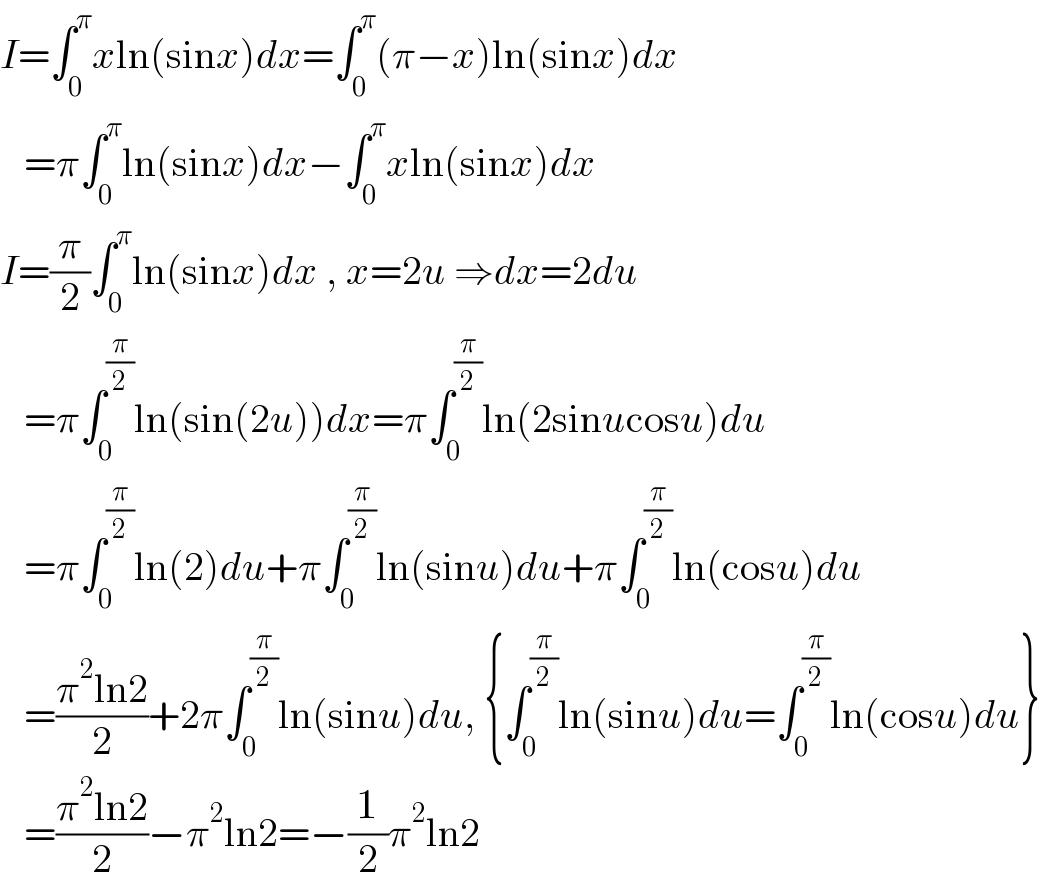
$${I}=\int_{\mathrm{0}} ^{\pi} {x}\mathrm{ln}\left(\mathrm{sin}{x}\right){dx}=\int_{\mathrm{0}} ^{\pi} \left(\pi−{x}\right)\mathrm{ln}\left(\mathrm{sin}{x}\right){dx} \\ $$$$\:\:\:=\pi\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{sin}{x}\right){dx}−\int_{\mathrm{0}} ^{\pi} {x}\mathrm{ln}\left(\mathrm{sin}{x}\right){dx} \\ $$$${I}=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{sin}{x}\right){dx}\:,\:{x}=\mathrm{2}{u}\:\Rightarrow{dx}=\mathrm{2}{du} \\ $$$$\:\:\:=\pi\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\left(\mathrm{2}{u}\right)\right){dx}=\pi\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{2sin}{u}\mathrm{cos}{u}\right){du} \\ $$$$\:\:\:=\pi\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{2}\right){du}+\pi\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{u}\right){du}+\pi\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cos}{u}\right){du} \\ $$$$\:\:\:=\frac{\pi^{\mathrm{2}} \mathrm{ln2}}{\mathrm{2}}+\mathrm{2}\pi\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{u}\right){du},\:\left\{\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{u}\right){du}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cos}{u}\right){du}\right\} \\ $$$$\:\:\:=\frac{\pi^{\mathrm{2}} \mathrm{ln2}}{\mathrm{2}}−\pi^{\mathrm{2}} \mathrm{ln2}=−\frac{\mathrm{1}}{\mathrm{2}}\pi^{\mathrm{2}} \mathrm{ln2} \\ $$
Commented by Ar Brandon last updated on 01/Jan/22
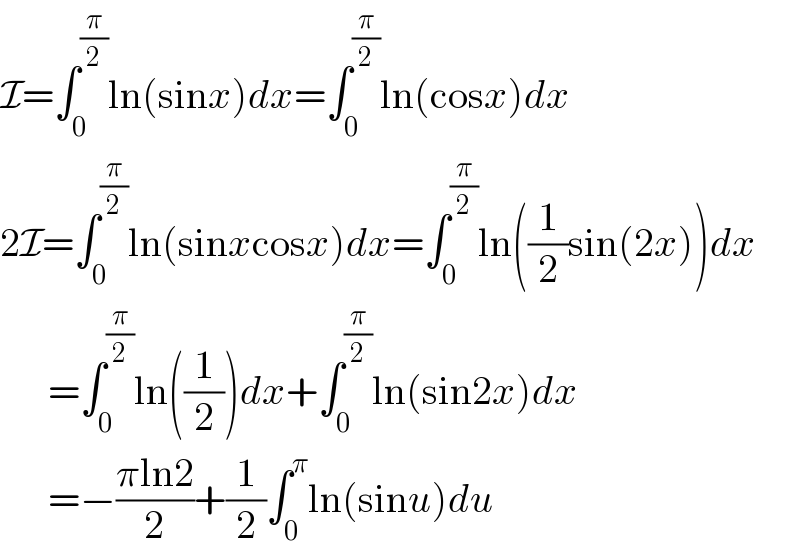
$$\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{x}\right){dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cos}{x}\right){dx} \\ $$$$\mathrm{2}\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{x}\mathrm{cos}{x}\right){dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}{x}\right)\right){dx} \\ $$$$\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){dx}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin2}{x}\right){dx} \\ $$$$\:\:\:\:\:\:=−\frac{\pi\mathrm{ln2}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{sin}{u}\right){du} \\ $$
Answered by Lordose last updated on 01/Jan/22
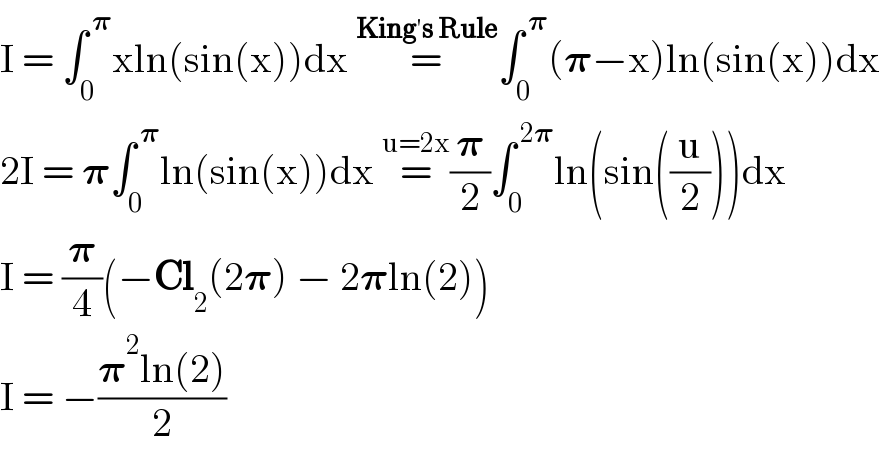
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\boldsymbol{\pi}} \mathrm{xln}\left(\mathrm{sin}\left(\mathrm{x}\right)\right)\mathrm{dx}\:\overset{\boldsymbol{\mathrm{King}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{Rule}}} {=}\int_{\mathrm{0}} ^{\:\boldsymbol{\pi}} \left(\boldsymbol{\pi}−\mathrm{x}\right)\mathrm{ln}\left(\mathrm{sin}\left(\mathrm{x}\right)\right)\mathrm{dx} \\ $$$$\mathrm{2I}\:=\:\boldsymbol{\pi}\int_{\mathrm{0}} ^{\:\boldsymbol{\pi}} \mathrm{ln}\left(\mathrm{sin}\left(\mathrm{x}\right)\right)\mathrm{dx}\:\overset{\mathrm{u}=\mathrm{2x}} {=}\frac{\boldsymbol{\pi}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{2}\boldsymbol{\pi}} \mathrm{ln}\left(\mathrm{sin}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)\right)\mathrm{dx} \\ $$$$\mathrm{I}\:=\:\frac{\boldsymbol{\pi}}{\mathrm{4}}\left(−\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} \left(\mathrm{2}\boldsymbol{\pi}\right)\:−\:\mathrm{2}\boldsymbol{\pi}\mathrm{ln}\left(\mathrm{2}\right)\right) \\ $$$$\mathrm{I}\:=\:−\frac{\boldsymbol{\pi}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$
Commented by mathacek last updated on 02/Jan/22

$${What}'{s}\:{for}\:\boldsymbol{\mathrm{Cl}}_{\mathrm{2}} ? \\ $$
Commented by Ar Brandon last updated on 02/Jan/22
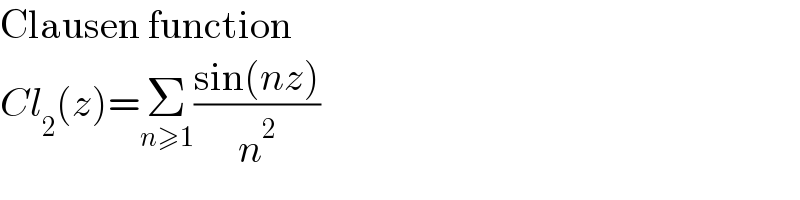
$$\mathrm{Clausen}\:\mathrm{function} \\ $$$${Cl}_{\mathrm{2}} \left({z}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{sin}\left({nz}\right)}{{n}^{\mathrm{2}} } \\ $$
