
Question Number 162382 by HongKing last updated on 29/Dec/21
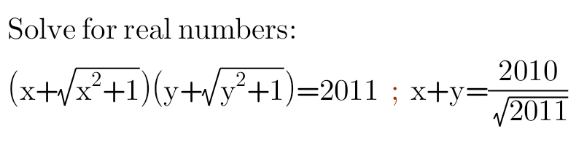
Answered by Rasheed.Sindhi last updated on 29/Dec/21
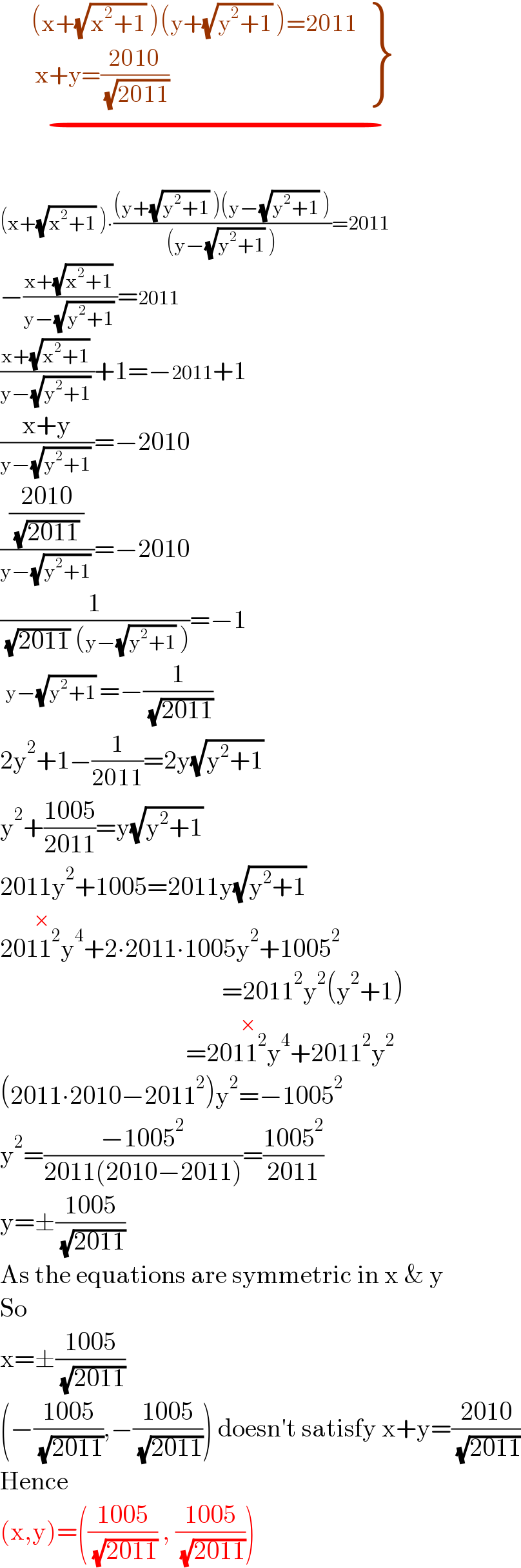
$$\underset{−} {\left.\begin{matrix}{\:\:\:\:\:\:\:\:\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\right)\left(\mathrm{y}+\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\:\right)=\mathrm{2011}}\\{\:\:\:\:\:\:\:\:\:\mathrm{x}+\mathrm{y}=\frac{\mathrm{2010}}{\:\sqrt{\mathrm{2011}}}\:\:}\end{matrix}\right\}\:\:\:\:\:\:\:\:\:\:}\:\: \\ $$$$\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\right)\centerdot\frac{\left(\mathrm{y}+\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\:\right)\left(\mathrm{y}−\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\:\right)}{\left(\mathrm{y}−\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\:\right)}=\mathrm{2011} \\ $$$$−\frac{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:}{\mathrm{y}−\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\:}=\mathrm{2011} \\ $$$$\frac{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:}{\mathrm{y}−\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\:}+\mathrm{1}=−\mathrm{2011}+\mathrm{1} \\ $$$$\frac{\mathrm{x}+\mathrm{y}}{\mathrm{y}−\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\:}=−\mathrm{2010} \\ $$$$\frac{\frac{\mathrm{2010}}{\:\sqrt{\mathrm{2011}}\:}}{\mathrm{y}−\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\:}=−\mathrm{2010} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2011}}\:\left(\mathrm{y}−\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\:\right)}=−\mathrm{1} \\ $$$$\:\mathrm{y}−\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\:=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2011}}} \\ $$$$\mathrm{2y}^{\mathrm{2}} +\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2011}}=\mathrm{2y}\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\: \\ $$$$\mathrm{y}^{\mathrm{2}} +\frac{\mathrm{1005}}{\mathrm{2011}}=\mathrm{y}\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\: \\ $$$$\mathrm{2011y}^{\mathrm{2}} +\mathrm{1005}=\mathrm{2011y}\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\: \\ $$$$\overset{×} {\mathrm{2011}^{\mathrm{2}} \mathrm{y}^{\mathrm{4}} }+\mathrm{2}\centerdot\mathrm{2011}\centerdot\mathrm{1005y}^{\mathrm{2}} +\mathrm{1005}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2011}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} \left(\mathrm{y}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\overset{×} {\mathrm{2011}^{\mathrm{2}} \mathrm{y}^{\mathrm{4}} }+\mathrm{2011}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} \\ $$$$\left(\mathrm{2011}\centerdot\mathrm{2010}−\mathrm{2011}^{\mathrm{2}} \right)\mathrm{y}^{\mathrm{2}} =−\mathrm{1005}^{\mathrm{2}} \\ $$$$\mathrm{y}^{\mathrm{2}} =\frac{−\mathrm{1005}^{\mathrm{2}} }{\mathrm{2011}\left(\mathrm{2010}−\mathrm{2011}\right)}=\frac{\mathrm{1005}^{\mathrm{2}} }{\mathrm{2011}} \\ $$$$\mathrm{y}=\pm\frac{\mathrm{1005}}{\:\sqrt{\mathrm{2011}}} \\ $$$$\mathrm{As}\:\mathrm{the}\:\mathrm{equations}\:\mathrm{are}\:\mathrm{symmetric}\:\mathrm{in}\:\mathrm{x}\:\&\:\mathrm{y} \\ $$$$\mathrm{So}\: \\ $$$$\mathrm{x}=\pm\frac{\mathrm{1005}}{\:\sqrt{\mathrm{2011}}} \\ $$$$\left(−\frac{\mathrm{1005}}{\:\sqrt{\mathrm{2011}}},−\frac{\mathrm{1005}}{\:\sqrt{\mathrm{2011}}}\right)\:\mathrm{doesn}'\mathrm{t}\:\mathrm{satisfy}\:\mathrm{x}+\mathrm{y}=\frac{\mathrm{2010}}{\:\sqrt{\mathrm{2011}}} \\ $$$$\mathrm{Hence} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\frac{\mathrm{1005}}{\:\sqrt{\mathrm{2011}}}\:,\:\frac{\mathrm{1005}}{\:\sqrt{\mathrm{2011}}}\right) \\ $$
Commented by HongKing last updated on 29/Dec/21
$$\mathrm{cool}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
Commented by mr W last updated on 29/Dec/21
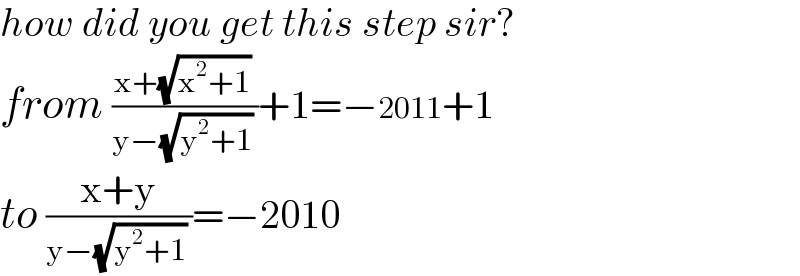
$${how}\:{did}\:{you}\:{get}\:{this}\:{step}\:{sir}? \\ $$$${from}\:\frac{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:}{\mathrm{y}−\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\:}+\mathrm{1}=−\mathrm{2011}+\mathrm{1} \\ $$$${to}\:\frac{\mathrm{x}+\mathrm{y}}{\mathrm{y}−\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}}\:}=−\mathrm{2010} \\ $$
Commented by mr W last updated on 29/Dec/21
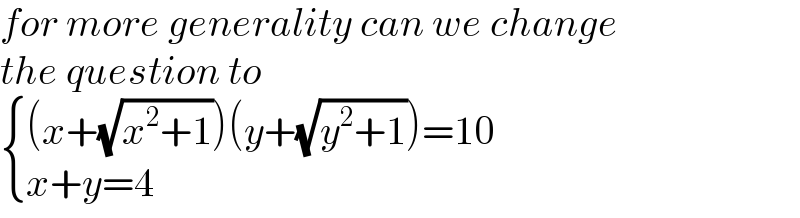
$${for}\:{more}\:{generality}\:{can}\:{we}\:{change} \\ $$$${the}\:{question}\:{to} \\ $$$$\begin{cases}{\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\left({y}+\sqrt{{y}^{\mathrm{2}} +\mathrm{1}}\right)=\mathrm{10}}\\{{x}+{y}=\mathrm{4}}\end{cases} \\ $$
Commented by Rasheed.Sindhi last updated on 29/Dec/21

$$\mathrm{Mistake}\:\boldsymbol{\mathrm{sir}}!\:\mathrm{I}\:\mathrm{considered}\:\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\&\:\sqrt{\mathrm{y}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\boldsymbol{\mathrm{same}}!\:\mathrm{I}\:\mathrm{was}\:\mathrm{very}\:\mathrm{happy}\:\mathrm{for}\:\mathrm{eliminating}\:\mathrm{x}, \\ $$$$\mathrm{but}\:\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{so}\:\mathrm{easy}.\: \\ $$😭😭😭
Commented by mr W last updated on 29/Dec/21
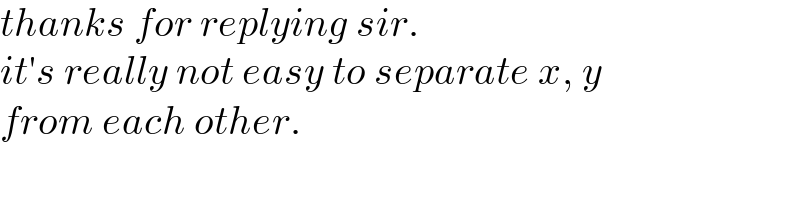
$${thanks}\:{for}\:{replying}\:{sir}. \\ $$$${it}'{s}\:{really}\:{not}\:{easy}\:{to}\:{separate}\:{x},\:{y} \\ $$$${from}\:{each}\:{other}. \\ $$
Commented by Rasheed.Sindhi last updated on 29/Dec/21

$${I}\:{wonder}\:\boldsymbol{{sir}},{that}\:{HongKing}\:{sir} \\ $$$${also}\:{hasn}'{t}\:{noticed}\:{it}!\:{Perhaps}\:{the} \\ $$$${answer}\:{is}\:{accidently}\:{correct}\:{or}\:{he} \\ $$$${hadn}'{t}\:{answer}\:{of}\:{the}\:{question}! \\ $$$${Anyway}\:{thanks}\:{for}\:{your}\:{keen}\:{observation}! \\ $$
Commented by mr W last updated on 29/Dec/21

$${the}\:{question}\:{is}\:{not}\:{general}\:{enough}. \\ $$$${both}\:{symmetric}\:{curves}\:{tangent}\:{each} \\ $$$${other},\:{so}\:{x}={y}\:{fulfills}\:{the}\:{solution}. \\ $$
Commented by Rasheed.Sindhi last updated on 29/Dec/21
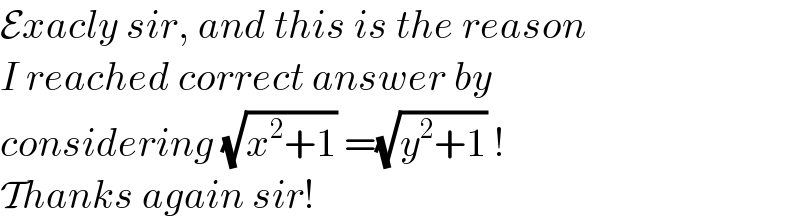
$$\mathcal{E}{xacly}\:{sir},\:{and}\:{this}\:{is}\:{the}\:{reason} \\ $$$${I}\:{reached}\:{correct}\:{answer}\:{by} \\ $$$${considering}\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:=\sqrt{{y}^{\mathrm{2}} +\mathrm{1}}\:! \\ $$$$\mathcal{T}{hanks}\:{again}\:{sir}! \\ $$
Commented by mr W last updated on 29/Dec/21
������
Commented by Ar Brandon last updated on 29/Dec/21
$$\mathrm{It}'\mathrm{s}\:\mathrm{really}\:\mathrm{not}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{separate}\:{x}\:\mathrm{and}\:{y}\: \\ $$$$\mathrm{from}\:\mathrm{each}\:\mathrm{other}.\:\mathrm{They}\:\mathrm{are}\:\mathrm{deeply}\:\mathrm{in}\:\mathrm{love} \\ $$🤗🤭
Answered by MJS_new last updated on 29/Dec/21
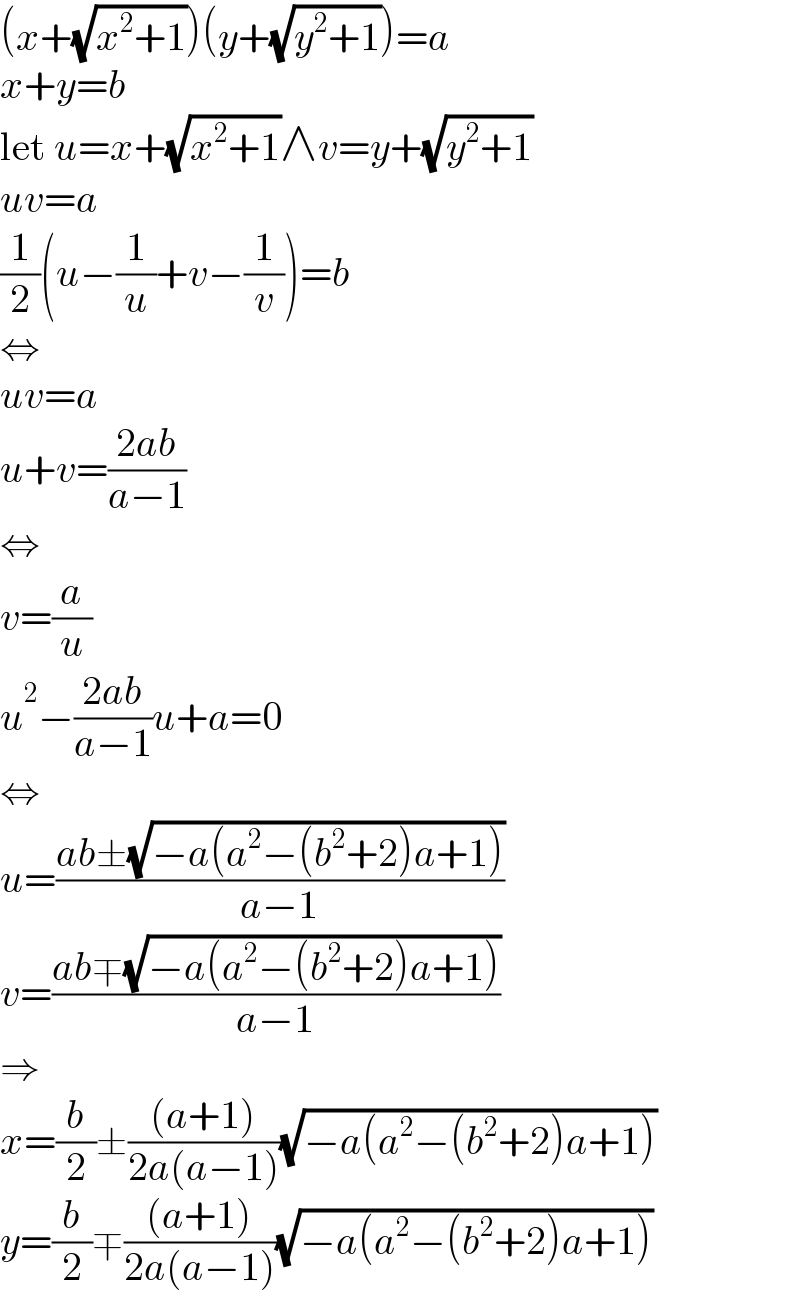
$$\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)\left({y}+\sqrt{{y}^{\mathrm{2}} +\mathrm{1}}\right)={a} \\ $$$${x}+{y}={b} \\ $$$$\mathrm{let}\:{u}={x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\wedge{v}={y}+\sqrt{{y}^{\mathrm{2}} +\mathrm{1}} \\ $$$${uv}={a} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({u}−\frac{\mathrm{1}}{{u}}+{v}−\frac{\mathrm{1}}{{v}}\right)={b} \\ $$$$\Leftrightarrow \\ $$$${uv}={a} \\ $$$${u}+{v}=\frac{\mathrm{2}{ab}}{{a}−\mathrm{1}} \\ $$$$\Leftrightarrow \\ $$$${v}=\frac{{a}}{{u}} \\ $$$${u}^{\mathrm{2}} −\frac{\mathrm{2}{ab}}{{a}−\mathrm{1}}{u}+{a}=\mathrm{0} \\ $$$$\Leftrightarrow \\ $$$${u}=\frac{{ab}\pm\sqrt{−{a}\left({a}^{\mathrm{2}} −\left({b}^{\mathrm{2}} +\mathrm{2}\right){a}+\mathrm{1}\right)}}{{a}−\mathrm{1}} \\ $$$${v}=\frac{{ab}\mp\sqrt{−{a}\left({a}^{\mathrm{2}} −\left({b}^{\mathrm{2}} +\mathrm{2}\right){a}+\mathrm{1}\right)}}{{a}−\mathrm{1}} \\ $$$$\Rightarrow \\ $$$${x}=\frac{{b}}{\mathrm{2}}\pm\frac{\left({a}+\mathrm{1}\right)}{\mathrm{2}{a}\left({a}−\mathrm{1}\right)}\sqrt{−{a}\left({a}^{\mathrm{2}} −\left({b}^{\mathrm{2}} +\mathrm{2}\right){a}+\mathrm{1}\right)} \\ $$$${y}=\frac{{b}}{\mathrm{2}}\mp\frac{\left({a}+\mathrm{1}\right)}{\mathrm{2}{a}\left({a}−\mathrm{1}\right)}\sqrt{−{a}\left({a}^{\mathrm{2}} −\left({b}^{\mathrm{2}} +\mathrm{2}\right){a}+\mathrm{1}\right)} \\ $$
Commented by mr W last updated on 29/Dec/21

$${great}! \\ $$
Commented by Tawa11 last updated on 30/Dec/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by HongKing last updated on 31/Dec/21

$$\mathrm{cool}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir} \\ $$
