
Question Number 161914 by mnjuly1970 last updated on 24/Dec/21
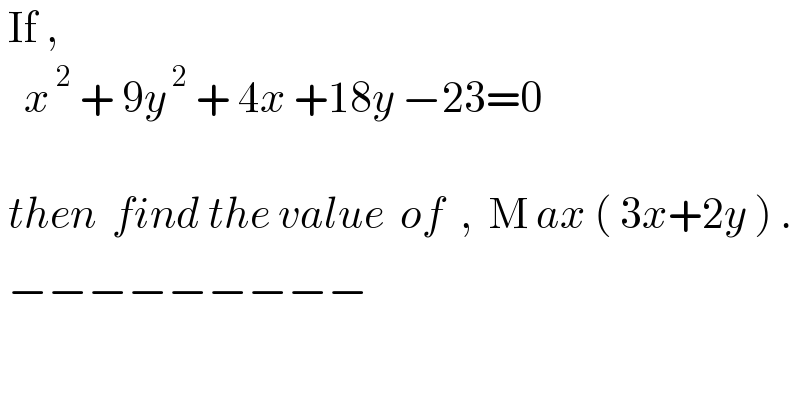
$$\:\mathrm{If}\:, \\ $$$$\:\:\:{x}^{\:\mathrm{2}} \:+\:\mathrm{9}{y}^{\:\mathrm{2}} \:+\:\mathrm{4}{x}\:+\mathrm{18}{y}\:−\mathrm{23}=\mathrm{0} \\ $$$$ \\ $$$$\:{then}\:\:{find}\:{the}\:{value}\:\:{of}\:\:,\:\:\mathrm{M}_{\:} {ax}\:\left(\:\mathrm{3}{x}+\mathrm{2}{y}\:\right)\:. \\ $$$$\:−−−−−−−−− \\ $$$$ \\ $$
Answered by mr W last updated on 24/Dec/21
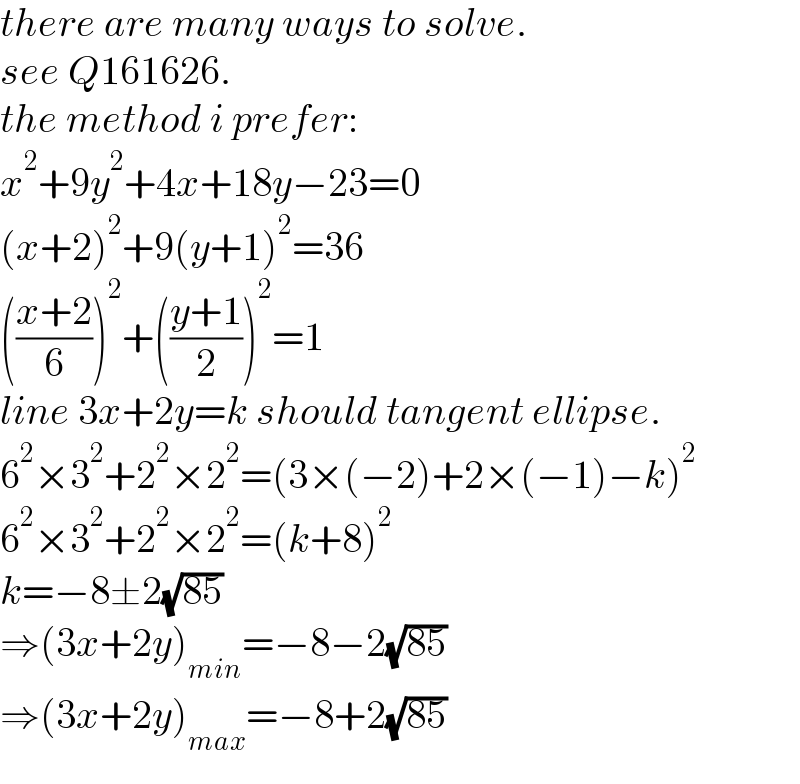
$${there}\:{are}\:{many}\:{ways}\:{to}\:{solve}. \\ $$$${see}\:{Q}\mathrm{161626}. \\ $$$${the}\:{method}\:{i}\:{prefer}: \\ $$$${x}^{\mathrm{2}} +\mathrm{9}{y}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{18}{y}−\mathrm{23}=\mathrm{0} \\ $$$$\left({x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{9}\left({y}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{36} \\ $$$$\left(\frac{{x}+\mathrm{2}}{\mathrm{6}}\right)^{\mathrm{2}} +\left(\frac{{y}+\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${line}\:\mathrm{3}{x}+\mathrm{2}{y}={k}\:{should}\:{tangent}\:{ellipse}. \\ $$$$\mathrm{6}^{\mathrm{2}} ×\mathrm{3}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{2}} =\left(\mathrm{3}×\left(−\mathrm{2}\right)+\mathrm{2}×\left(−\mathrm{1}\right)−{k}\right)^{\mathrm{2}} \\ $$$$\mathrm{6}^{\mathrm{2}} ×\mathrm{3}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{2}} =\left({k}+\mathrm{8}\right)^{\mathrm{2}} \\ $$$${k}=−\mathrm{8}\pm\mathrm{2}\sqrt{\mathrm{85}} \\ $$$$\Rightarrow\left(\mathrm{3}{x}+\mathrm{2}{y}\right)_{{min}} =−\mathrm{8}−\mathrm{2}\sqrt{\mathrm{85}} \\ $$$$\Rightarrow\left(\mathrm{3}{x}+\mathrm{2}{y}\right)_{{max}} =−\mathrm{8}+\mathrm{2}\sqrt{\mathrm{85}} \\ $$
Commented by mnjuly1970 last updated on 24/Dec/21
$${thanks}\:{alot}\:{sir}\:{W}. \\ $$
