
Question Number 161675 by cortano last updated on 21/Dec/21
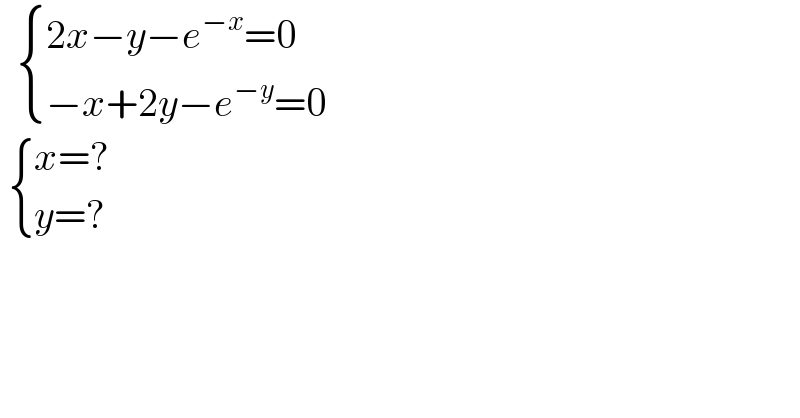
$$\:\:\begin{cases}{\mathrm{2}{x}−{y}−{e}^{−{x}} =\mathrm{0}}\\{−{x}+\mathrm{2}{y}−{e}^{−{y}} =\mathrm{0}}\end{cases} \\ $$$$\:\begin{cases}{{x}=?}\\{{y}=?}\end{cases} \\ $$
Answered by mr W last updated on 21/Dec/21
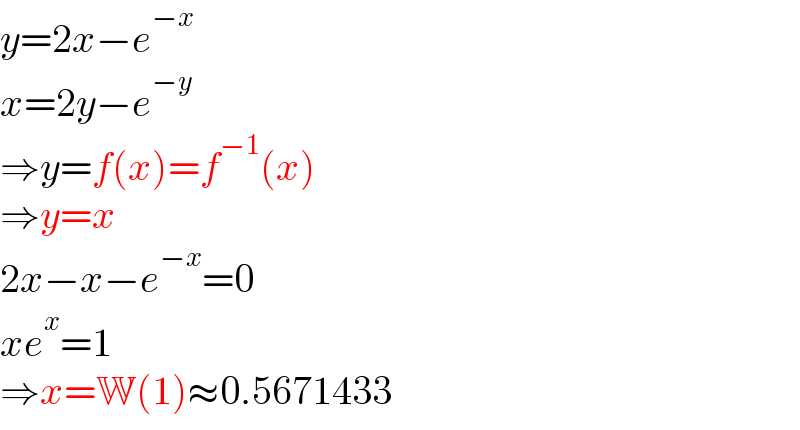
$${y}=\mathrm{2}{x}−{e}^{−{x}} \\ $$$${x}=\mathrm{2}{y}−{e}^{−{y}} \\ $$$$\Rightarrow{y}={f}\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right) \\ $$$$\Rightarrow{y}={x} \\ $$$$\mathrm{2}{x}−{x}−{e}^{−{x}} =\mathrm{0} \\ $$$${xe}^{{x}} =\mathrm{1} \\ $$$$\Rightarrow{x}=\mathbb{W}\left(\mathrm{1}\right)\approx\mathrm{0}.\mathrm{5671433} \\ $$
Commented by cortano last updated on 21/Dec/21
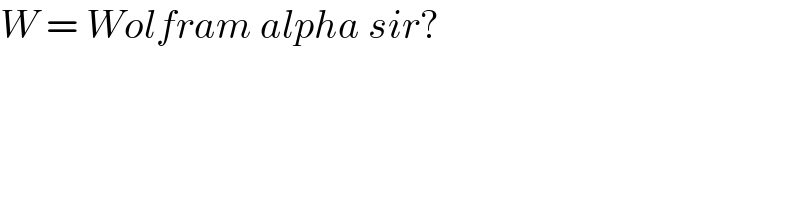
$${W}\:=\:{Wolfram}\:{alpha}\:{sir}? \\ $$
Commented by cortano last updated on 21/Dec/21
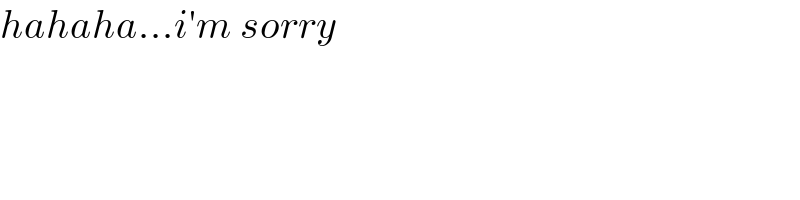
$${hahaha}...{i}'{m}\:{sorry} \\ $$
Commented by Ar Brandon last updated on 21/Dec/21
������
Commented by Ar Brandon last updated on 21/Dec/21
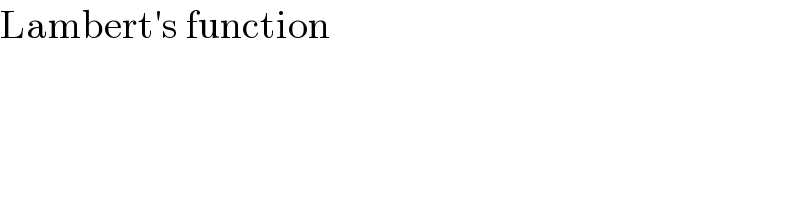
$$\mathrm{Lambert}'\mathrm{s}\:\mathrm{function} \\ $$
Commented by mr W last updated on 21/Dec/21

$${mr}\:\boldsymbol{\mathcal{W}}\:{has}\:{nothing}\:{to}\:{do}\:{with} \\ $$$${Wolfram}\:{alpha}/{beta}/{gamma} \\ $$$$\left./{delta}/{omicron}\:{etc}.\:\::\right) \\ $$
Commented by Ar Brandon last updated on 21/Dec/21
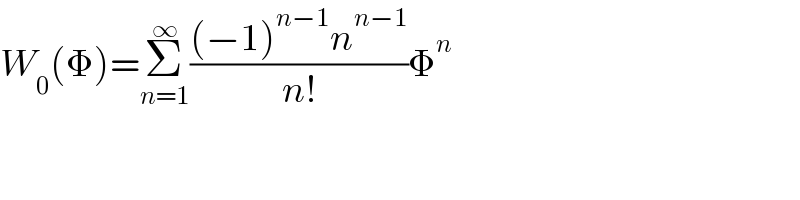
$${W}_{\mathrm{0}} \left(\Phi\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {n}^{{n}−\mathrm{1}} }{{n}!}\Phi^{{n}} \: \\ $$
Commented by Ar Brandon last updated on 21/Dec/21
��
Commented by cortano last updated on 21/Dec/21

$${haha}\:{covid}\:\mathrm{19} \\ $$
Commented by aleks041103 last updated on 24/Dec/21
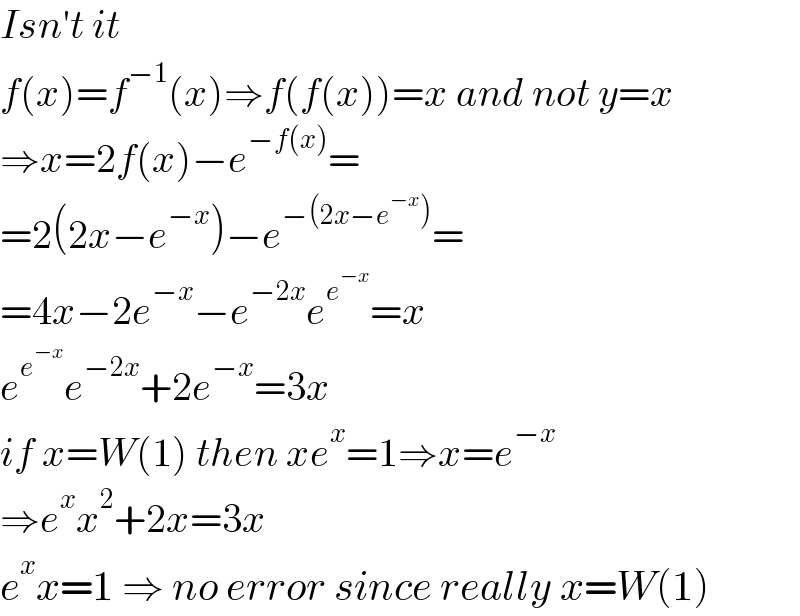
$${Isn}'{t}\:{it} \\ $$$${f}\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right)\Rightarrow{f}\left({f}\left({x}\right)\right)={x}\:{and}\:{not}\:{y}={x} \\ $$$$\Rightarrow{x}=\mathrm{2}{f}\left({x}\right)−{e}^{−{f}\left({x}\right)} = \\ $$$$=\mathrm{2}\left(\mathrm{2}{x}−{e}^{−{x}} \right)−{e}^{−\left(\mathrm{2}{x}−{e}^{−{x}} \right)} = \\ $$$$=\mathrm{4}{x}−\mathrm{2}{e}^{−{x}} −{e}^{−\mathrm{2}{x}} {e}^{{e}^{−{x}} } ={x} \\ $$$${e}^{{e}^{−{x}} } {e}^{−\mathrm{2}{x}} +\mathrm{2}{e}^{−{x}} =\mathrm{3}{x} \\ $$$${if}\:{x}={W}\left(\mathrm{1}\right)\:{then}\:{xe}^{{x}} =\mathrm{1}\Rightarrow{x}={e}^{−{x}} \\ $$$$\Rightarrow{e}^{{x}} {x}^{\mathrm{2}} +\mathrm{2}{x}=\mathrm{3}{x} \\ $$$${e}^{{x}} {x}=\mathrm{1}\:\Rightarrow\:{no}\:{error}\:{since}\:{really}\:{x}={W}\left(\mathrm{1}\right) \\ $$
