
Question Number 161671 by saly last updated on 21/Dec/21
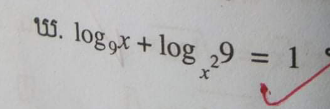
Commented by saly last updated on 21/Dec/21

$$\:\:\:\:{Do}\:{you}\:{help}\:{me}? \\ $$
Answered by Rasheed.Sindhi last updated on 21/Dec/21
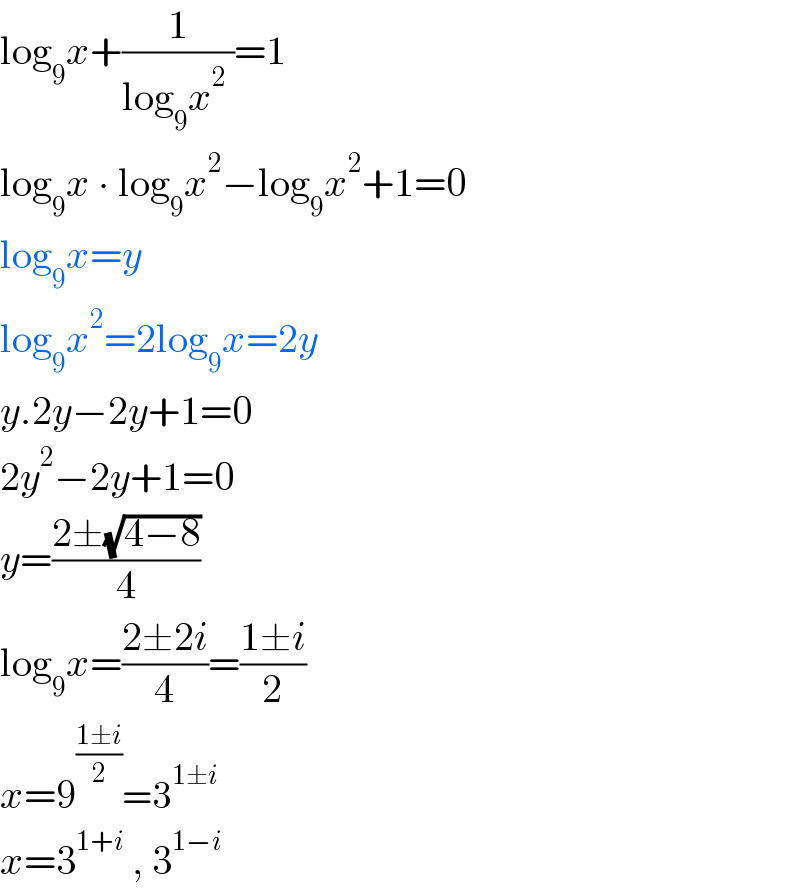
$$\mathrm{log}_{\mathrm{9}} {x}+\frac{\mathrm{1}}{\mathrm{log}_{\mathrm{9}} {x}^{\mathrm{2}} \:}=\mathrm{1} \\ $$$$\mathrm{log}_{\mathrm{9}} {x}\:\centerdot\:\mathrm{log}_{\mathrm{9}} {x}^{\mathrm{2}} −\mathrm{log}_{\mathrm{9}} {x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{log}_{\mathrm{9}} {x}={y} \\ $$$$\mathrm{log}_{\mathrm{9}} {x}^{\mathrm{2}} =\mathrm{2log}_{\mathrm{9}} {x}=\mathrm{2}{y} \\ $$$${y}.\mathrm{2}{y}−\mathrm{2}{y}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{2}{y}^{\mathrm{2}} −\mathrm{2}{y}+\mathrm{1}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{8}}}{\mathrm{4}} \\ $$$$\mathrm{log}_{\mathrm{9}} {x}=\frac{\mathrm{2}\pm\mathrm{2}{i}}{\mathrm{4}}=\frac{\mathrm{1}\pm{i}}{\mathrm{2}} \\ $$$${x}=\mathrm{9}^{\frac{\mathrm{1}\pm{i}}{\mathrm{2}}} =\mathrm{3}^{\mathrm{1}\pm{i}} \\ $$$${x}=\mathrm{3}^{\mathrm{1}+{i}} \:,\:\mathrm{3}^{\mathrm{1}−{i}} \\ $$
Answered by cortano last updated on 21/Dec/21
![log _9 (x)+log _((x^2 )) (9) =1 log _9 (x)+(1/(2log _9 (x))) =1 [ log _9 (x)=y , x>0 &x≠1 ] y+(1/(2y))=1⇒2y^2 −2y+1=0 y^2 −y+(1/2)=0 (y−(1/2))^2 +(1/4)=0 no solution](Q161677.png)
$$\:\mathrm{log}\:_{\mathrm{9}} \left({x}\right)+\mathrm{log}\:_{\left({x}^{\mathrm{2}} \right)} \left(\mathrm{9}\right)\:=\mathrm{1} \\ $$$$\:\mathrm{log}\:_{\mathrm{9}} \left({x}\right)+\frac{\mathrm{1}}{\mathrm{2log}\:_{\mathrm{9}} \left({x}\right)}\:=\mathrm{1} \\ $$$$\:\left[\:\mathrm{log}\:_{\mathrm{9}} \left({x}\right)={y}\:,\:{x}>\mathrm{0}\:\&{x}\neq\mathrm{1}\:\right] \\ $$$$\:{y}+\frac{\mathrm{1}}{\mathrm{2}{y}}=\mathrm{1}\Rightarrow\mathrm{2}{y}^{\mathrm{2}} −\mathrm{2}{y}+\mathrm{1}=\mathrm{0} \\ $$$$\:{y}^{\mathrm{2}} −{y}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\:\left({y}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\:{no}\:{solution} \\ $$
Commented by saly last updated on 21/Dec/21

$$\:\:\:\:{okay}\:\:,\:{Thank}\:{you} \\ $$
