
Question Number 161563 by HongKing last updated on 19/Dec/21
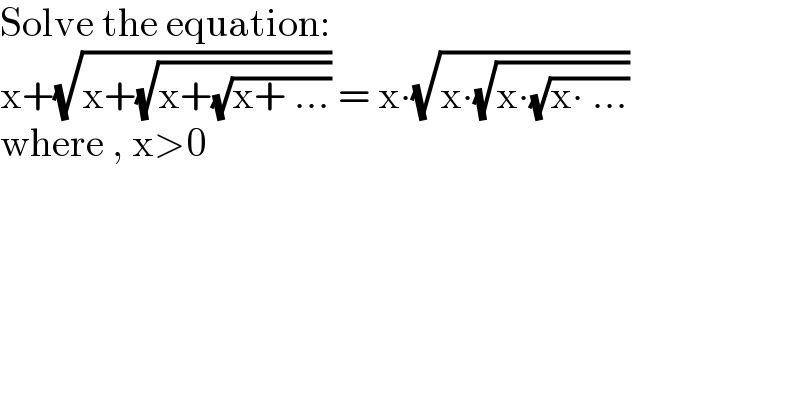
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}: \\ $$ $$\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\:...}}}\:=\:\mathrm{x}\centerdot\sqrt{\mathrm{x}\centerdot\sqrt{\mathrm{x}\centerdot\sqrt{\mathrm{x}\centerdot\:...}}} \\ $$ $$\mathrm{where}\:,\:\mathrm{x}>\mathrm{0} \\ $$
Answered by MJS_new last updated on 20/Dec/21
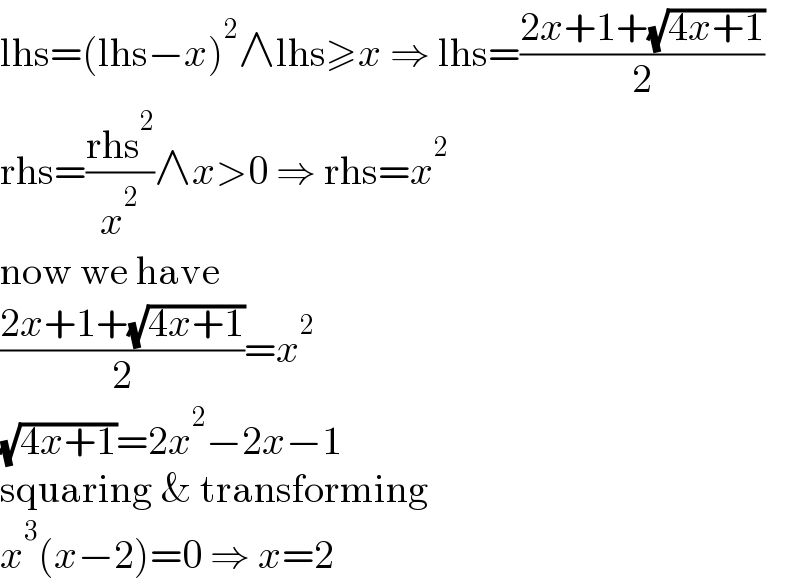
$$\mathrm{lhs}=\left(\mathrm{lhs}−{x}\right)^{\mathrm{2}} \wedge\mathrm{lhs}\geqslant{x}\:\Rightarrow\:\mathrm{lhs}=\frac{\mathrm{2}{x}+\mathrm{1}+\sqrt{\mathrm{4}{x}+\mathrm{1}}}{\mathrm{2}} \\ $$ $$\mathrm{rhs}=\frac{\mathrm{rhs}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\wedge{x}>\mathrm{0}\:\Rightarrow\:\mathrm{rhs}={x}^{\mathrm{2}} \\ $$ $$\mathrm{now}\:\mathrm{we}\:\mathrm{have} \\ $$ $$\frac{\mathrm{2}{x}+\mathrm{1}+\sqrt{\mathrm{4}{x}+\mathrm{1}}}{\mathrm{2}}={x}^{\mathrm{2}} \\ $$ $$\sqrt{\mathrm{4}{x}+\mathrm{1}}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1} \\ $$ $$\mathrm{squaring}\:\&\:\mathrm{transforming} \\ $$ $${x}^{\mathrm{3}} \left({x}−\mathrm{2}\right)=\mathrm{0}\:\Rightarrow\:{x}=\mathrm{2} \\ $$
Commented byHongKing last updated on 20/Dec/21
$$\mathrm{very}\:\mathrm{nice}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you} \\ $$
