Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 161280 by HongKing last updated on 15/Dec/21

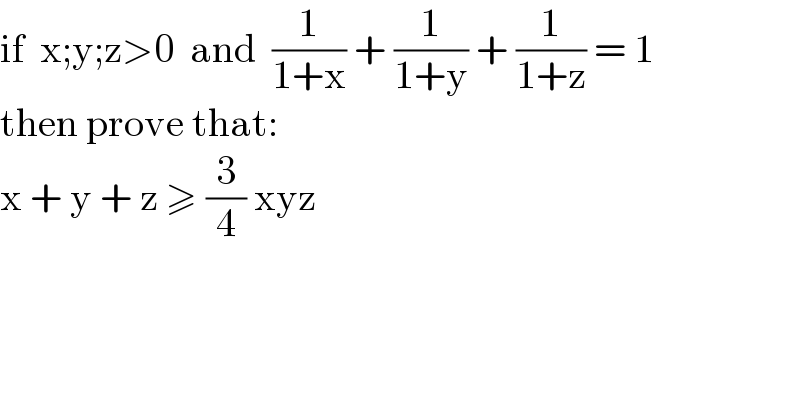
if x;y;z>0 and (1/(1+x)) + (1/(1+y)) + (1/(1+z)) = 1 then prove that: x + y + z ≥ (3/4) xyz

$$\mathrm{if}\:\:\mathrm{x};\mathrm{y};\mathrm{z}>\mathrm{0}\:\:\mathrm{and}\:\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\:+\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{y}}\:+\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{z}}\:=\:\mathrm{1} \\ $$ $$\mathrm{then}\:\mathrm{prove}\:\mathrm{that}: \\ $$ $$\mathrm{x}\:+\:\mathrm{y}\:+\:\mathrm{z}\:\geqslant\:\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{xyz} \\ $$

Answered by 1549442205PVT last updated on 16/Dec/21

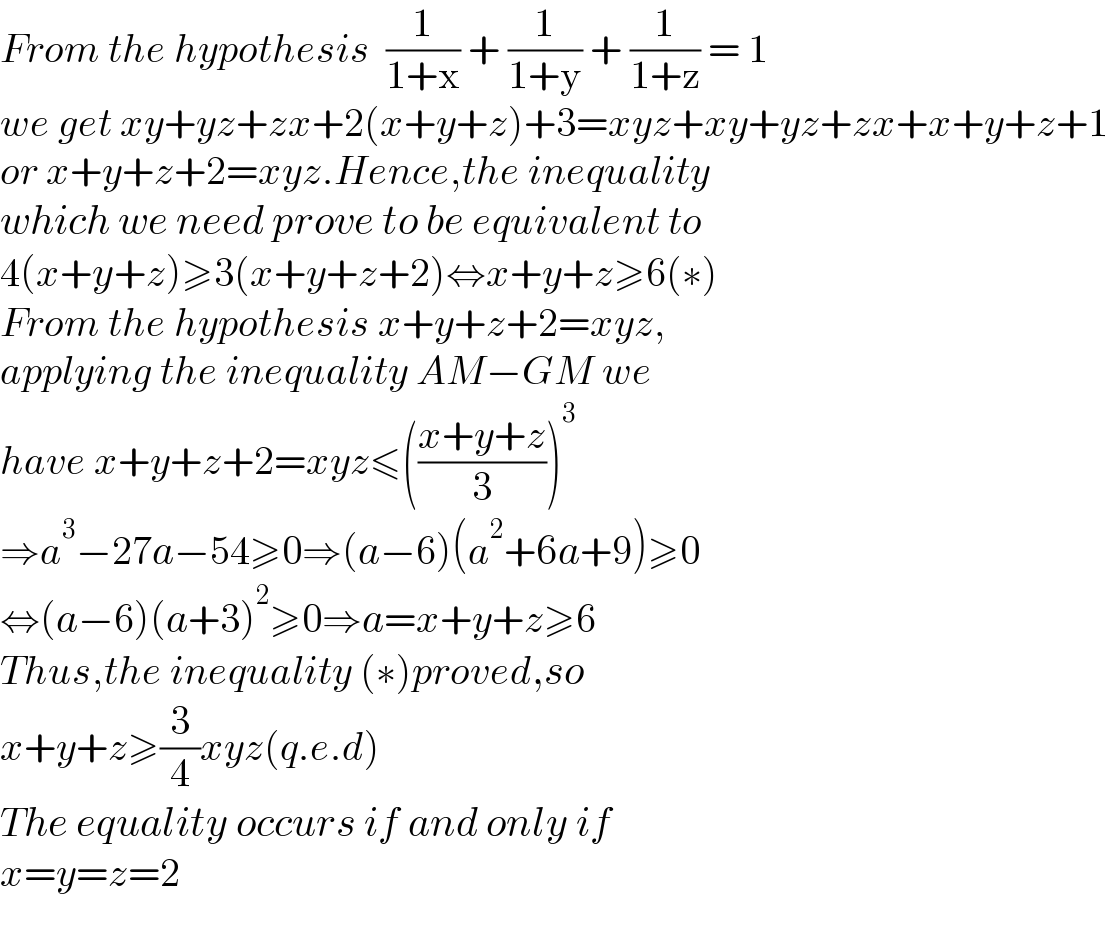
From the hypothesis (1/(1+x)) + (1/(1+y)) + (1/(1+z)) = 1 we get xy+yz+zx+2(x+y+z)+3=xyz+xy+yz+zx+x+y+z+1 or x+y+z+2=xyz.Hence,the inequality which we need prove to be equivalent to 4(x+y+z)≥3(x+y+z+2)⇔x+y+z≥6(∗) From the hypothesis x+y+z+2=xyz, applying the inequality AM−GM we have x+y+z+2=xyz≤(((x+y+z)/3))^3 ⇒a^3 −27a−54≥0⇒(a−6)(a^2 +6a+9)≥0 ⇔(a−6)(a+3)^2 ≥0⇒a=x+y+z≥6 Thus,the inequality (∗)proved,so x+y+z≥(3/4)xyz(q.e.d) The equality occurs if and only if x=y=z=2

$${From}\:{the}\:{hypothesis}\:\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\:+\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{y}}\:+\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{z}}\:=\:\mathrm{1} \\ $$ $${we}\:{get}\:{xy}+{yz}+{zx}+\mathrm{2}\left({x}+{y}+{z}\right)+\mathrm{3}={xyz}+{xy}+{yz}+{zx}+{x}+{y}+{z}+\mathrm{1} \\ $$ $${or}\:{x}+{y}+{z}+\mathrm{2}={xyz}.{Hence},{the}\:{inequality} \\ $$ $${which}\:{we}\:{need}\:{prove}\:{to}\:{be}\:{equivalent}\:{to}\: \\ $$ $$\mathrm{4}\left({x}+{y}+{z}\right)\geqslant\mathrm{3}\left({x}+{y}+{z}+\mathrm{2}\right)\Leftrightarrow{x}+{y}+{z}\geqslant\mathrm{6}\left(\ast\right) \\ $$ $${From}\:{the}\:{hypothesis}\:{x}+{y}+{z}+\mathrm{2}={xyz}, \\ $$ $${applying}\:{the}\:{inequality}\:{AM}−{GM}\:{we} \\ $$ $${have}\:{x}+{y}+{z}+\mathrm{2}={xyz}\leqslant\left(\frac{{x}+{y}+{z}}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$ $$\Rightarrow{a}^{\mathrm{3}} −\mathrm{27}{a}−\mathrm{54}\geqslant\mathrm{0}\Rightarrow\left({a}−\mathrm{6}\right)\left({a}^{\mathrm{2}} +\mathrm{6}{a}+\mathrm{9}\right)\geqslant\mathrm{0} \\ $$ $$\Leftrightarrow\left({a}−\mathrm{6}\right)\left({a}+\mathrm{3}\right)^{\mathrm{2}} \geqslant\mathrm{0}\Rightarrow{a}={x}+{y}+{z}\geqslant\mathrm{6} \\ $$ $${Thus},{the}\:{inequality}\:\left(\ast\right){proved},{so} \\ $$ $${x}+{y}+{z}\geqslant\frac{\mathrm{3}}{\mathrm{4}}{xyz}\left({q}.{e}.{d}\right) \\ $$ $${The}\:{equality}\:{occurs}\:{if}\:{and}\:{only}\:{if} \\ $$ $${x}={y}={z}=\mathrm{2} \\ $$

Commented byHongKing last updated on 17/Dec/21

perfect my dear Sir thank you

$$\mathrm{perfect}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com