
Question Number 160325 by NUR23 last updated on 27/Nov/21
Commented by NUR23 last updated on 27/Nov/21
$${By}\:{the}\:{name}\:{of}\:{odin}\:{plz}\:{help}\:{me} \\ $$$$ \\ $$
Commented by mr W last updated on 29/Nov/21

$${yesterday}\:{i}\:{saw}\:{a}\:{man}\:{crying}\:{loudly} \\ $$$${for}\:{help}\:{on}\:{the}\:{street}.\:{then}\:{people} \\ $$$${came}\:{and}\:{helped}\:{ihm}.\:{what}\:{did}\:{the} \\ $$$${man}?\:{nothing}!\:{he}\:{spoke}\:{no}\:{word}\:{as} \\ $$$${if}\:{he}\:{were}\:{dump}.\:{he}\:{neither}\:{thanked} \\ $$$${the}\:{people}\:{who}\:{helped}\:{him}\:{nor}\:{told}\:{if} \\ $$$${the}\:{problem}\:{he}\:{had}\:{was}\:{gone}.\:{i}\:{guess} \\ $$$${next}\:{time}\:{when}\:{he}\:{cries}\:{for}\:{help} \\ $$$${again},\:{not}\:{so}\:{many}\:{people}\:{will}\:{come} \\ $$$${to}\:{help}\:{him}. \\ $$
Commented by Tawa11 last updated on 03/Dec/21

$$\mathrm{That}\:\mathrm{is}\:\mathrm{human}\:\mathrm{being}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{personally}\:\mathrm{love}\:\mathrm{your}\:\mathrm{geometry}\:\mathrm{solutions}\:\mathrm{sir}. \\ $$$$\mathrm{That}\:\mathrm{is}\:\mathrm{why}\:\mathrm{I}\:\mathrm{follow}\:\mathrm{your}\:\mathrm{solutions}\:\mathrm{everytime}.\: \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by mr W last updated on 27/Nov/21
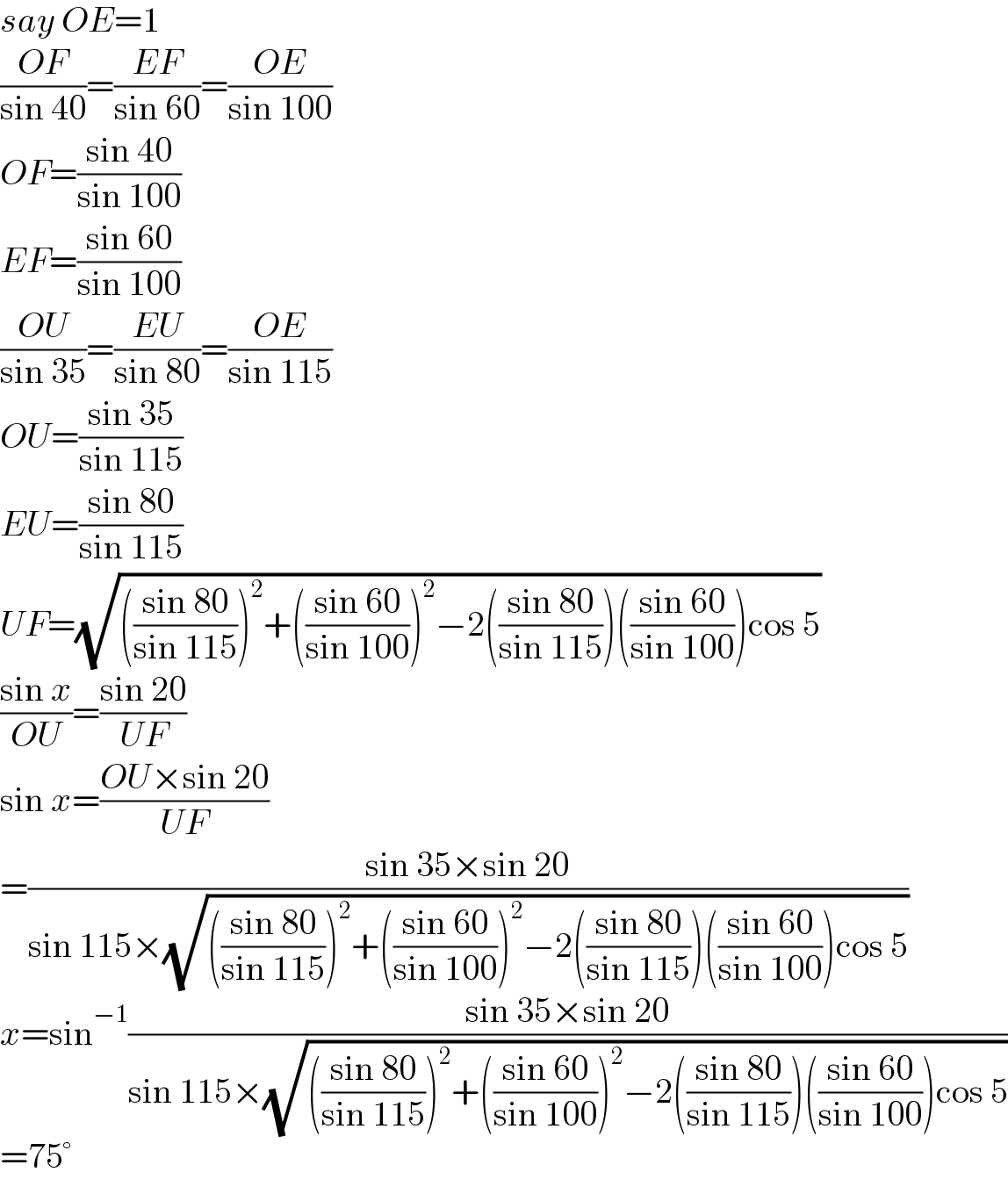
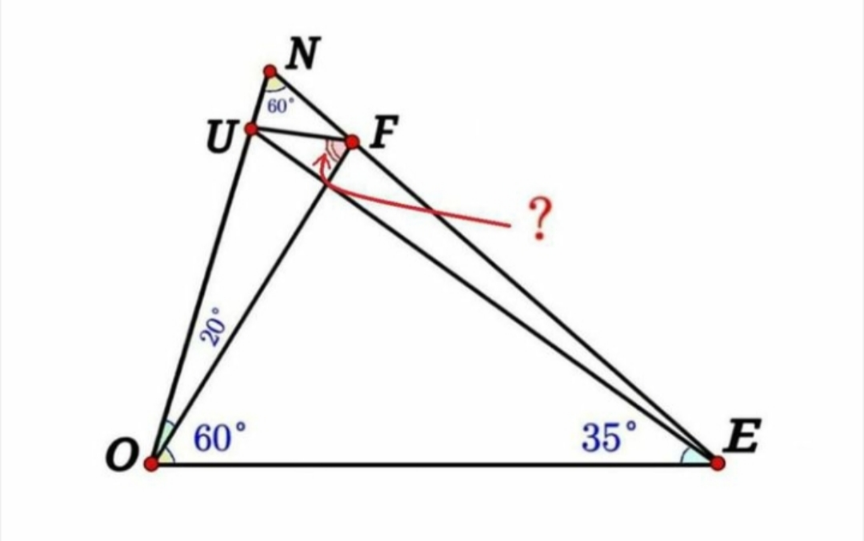
$${say}\:{OE}=\mathrm{1} \\ $$$$\frac{{OF}}{\mathrm{sin}\:\mathrm{40}}=\frac{{EF}}{\mathrm{sin}\:\mathrm{60}}=\frac{{OE}}{\mathrm{sin}\:\mathrm{100}} \\ $$$${OF}=\frac{\mathrm{sin}\:\mathrm{40}}{\mathrm{sin}\:\mathrm{100}} \\ $$$${EF}=\frac{\mathrm{sin}\:\mathrm{60}}{\mathrm{sin}\:\mathrm{100}} \\ $$$$\frac{{OU}}{\mathrm{sin}\:\mathrm{35}}=\frac{{EU}}{\mathrm{sin}\:\mathrm{80}}=\frac{{OE}}{\mathrm{sin}\:\mathrm{115}} \\ $$$${OU}=\frac{\mathrm{sin}\:\mathrm{35}}{\mathrm{sin}\:\mathrm{115}} \\ $$$${EU}=\frac{\mathrm{sin}\:\mathrm{80}}{\mathrm{sin}\:\mathrm{115}} \\ $$$${UF}=\sqrt{\left(\frac{\mathrm{sin}\:\mathrm{80}}{\mathrm{sin}\:\mathrm{115}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{sin}\:\mathrm{60}}{\mathrm{sin}\:\mathrm{100}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{sin}\:\mathrm{80}}{\mathrm{sin}\:\mathrm{115}}\right)\left(\frac{\mathrm{sin}\:\mathrm{60}}{\mathrm{sin}\:\mathrm{100}}\right)\mathrm{cos}\:\mathrm{5}} \\ $$$$\frac{\mathrm{sin}\:{x}}{{OU}}=\frac{\mathrm{sin}\:\mathrm{20}}{{UF}} \\ $$$$\mathrm{sin}\:{x}=\frac{{OU}×\mathrm{sin}\:\mathrm{20}}{{UF}} \\ $$$$=\frac{\mathrm{sin}\:\mathrm{35}×\mathrm{sin}\:\mathrm{20}}{\mathrm{sin}\:\mathrm{115}×\sqrt{\left(\frac{\mathrm{sin}\:\mathrm{80}}{\mathrm{sin}\:\mathrm{115}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{sin}\:\mathrm{60}}{\mathrm{sin}\:\mathrm{100}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{sin}\:\mathrm{80}}{\mathrm{sin}\:\mathrm{115}}\right)\left(\frac{\mathrm{sin}\:\mathrm{60}}{\mathrm{sin}\:\mathrm{100}}\right)\mathrm{cos}\:\mathrm{5}}} \\ $$$${x}=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{sin}\:\mathrm{35}×\mathrm{sin}\:\mathrm{20}}{\mathrm{sin}\:\mathrm{115}×\sqrt{\left(\frac{\mathrm{sin}\:\mathrm{80}}{\mathrm{sin}\:\mathrm{115}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{sin}\:\mathrm{60}}{\mathrm{sin}\:\mathrm{100}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{sin}\:\mathrm{80}}{\mathrm{sin}\:\mathrm{115}}\right)\left(\frac{\mathrm{sin}\:\mathrm{60}}{\mathrm{sin}\:\mathrm{100}}\right)\mathrm{cos}\:\mathrm{5}}} \\ $$$$=\mathrm{75}° \\ $$
Commented by Tawa11 last updated on 28/Nov/21

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by NUR23 last updated on 08/Mar/22
$${thank}\:{you}\:{very}\:{much}\:{sir}\:{i}\:{was}\:{out}\:{lf}\:{the}?{line} \\ $$
