
Previous in Differential Equation Next in Differential Equation
Question Number 158309 by cortano last updated on 02/Nov/21
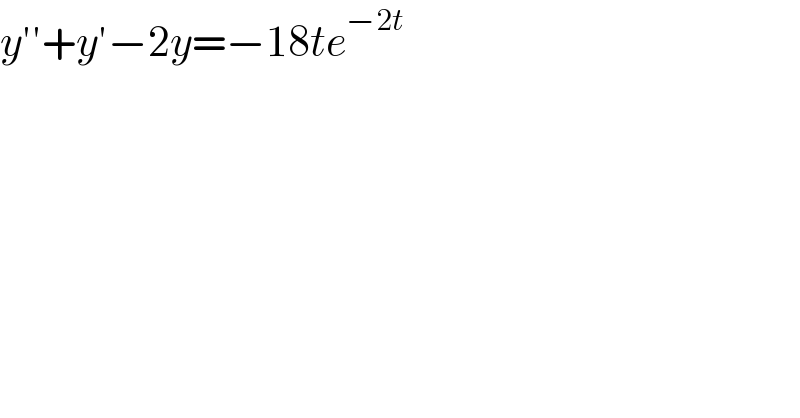
$${y}''+{y}'−\mathrm{2}{y}=−\mathrm{18}{te}^{−\mathrm{2}{t}} \\ $$
Answered by TheSupreme last updated on 02/Nov/21
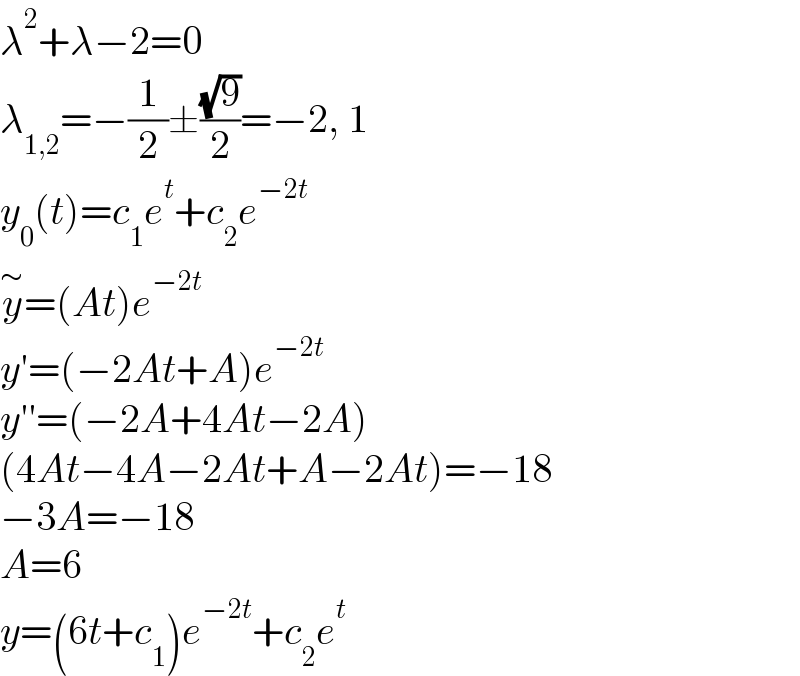
$$\lambda^{\mathrm{2}} +\lambda−\mathrm{2}=\mathrm{0} \\ $$$$\lambda_{\mathrm{1},\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{9}}}{\mathrm{2}}=−\mathrm{2},\:\mathrm{1} \\ $$$${y}_{\mathrm{0}} \left({t}\right)={c}_{\mathrm{1}} {e}^{{t}} +{c}_{\mathrm{2}} {e}^{−\mathrm{2}{t}} \\ $$$$\overset{\sim} {{y}}=\left({At}\right){e}^{−\mathrm{2}{t}} \\ $$$${y}'=\left(−\mathrm{2}{At}+{A}\right){e}^{−\mathrm{2}{t}} \\ $$$${y}''=\left(−\mathrm{2}{A}+\mathrm{4}{At}−\mathrm{2}{A}\right) \\ $$$$\left(\mathrm{4}{At}−\mathrm{4}{A}−\mathrm{2}{At}+{A}−\mathrm{2}{At}\right)=−\mathrm{18} \\ $$$$−\mathrm{3}{A}=−\mathrm{18} \\ $$$${A}=\mathrm{6} \\ $$$${y}=\left(\mathrm{6}{t}+{c}_{\mathrm{1}} \right){e}^{−\mathrm{2}{t}} +{c}_{\mathrm{2}} {e}^{{t}} \\ $$
Answered by tounghoungko last updated on 03/Nov/21
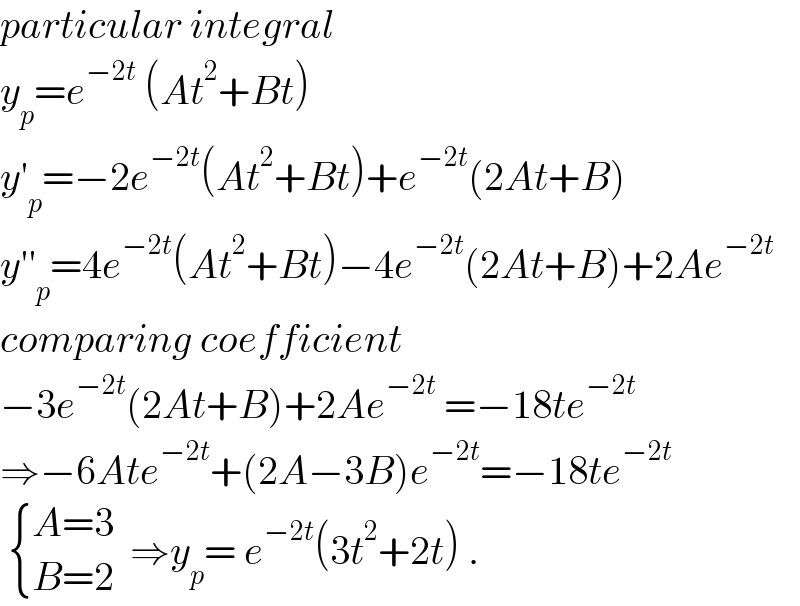
$${particular}\:{integral}\: \\ $$$${y}_{{p}} ={e}^{−\mathrm{2}{t}} \:\left({At}^{\mathrm{2}} +{Bt}\right) \\ $$$${y}'_{{p}} =−\mathrm{2}{e}^{−\mathrm{2}{t}} \left({At}^{\mathrm{2}} +{Bt}\right)+{e}^{−\mathrm{2}{t}} \left(\mathrm{2}{At}+{B}\right) \\ $$$${y}''_{{p}} =\mathrm{4}{e}^{−\mathrm{2}{t}} \left({At}^{\mathrm{2}} +{Bt}\right)−\mathrm{4}{e}^{−\mathrm{2}{t}} \left(\mathrm{2}{At}+{B}\right)+\mathrm{2}{Ae}^{−\mathrm{2}{t}} \\ $$$${comparing}\:{coefficient} \\ $$$$−\mathrm{3}{e}^{−\mathrm{2}{t}} \left(\mathrm{2}{At}+{B}\right)+\mathrm{2}{Ae}^{−\mathrm{2}{t}} \:=−\mathrm{18}{te}^{−\mathrm{2}{t}} \\ $$$$\Rightarrow−\mathrm{6}{Ate}^{−\mathrm{2}{t}} +\left(\mathrm{2}{A}−\mathrm{3}{B}\right){e}^{−\mathrm{2}{t}} =−\mathrm{18}{te}^{−\mathrm{2}{t}} \\ $$$$\:\begin{cases}{{A}=\mathrm{3}}\\{{B}=\mathrm{2}}\end{cases}\:\:\Rightarrow{y}_{{p}} =\:{e}^{−\mathrm{2}{t}} \left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}\right)\:. \\ $$
Answered by qaz last updated on 03/Nov/21
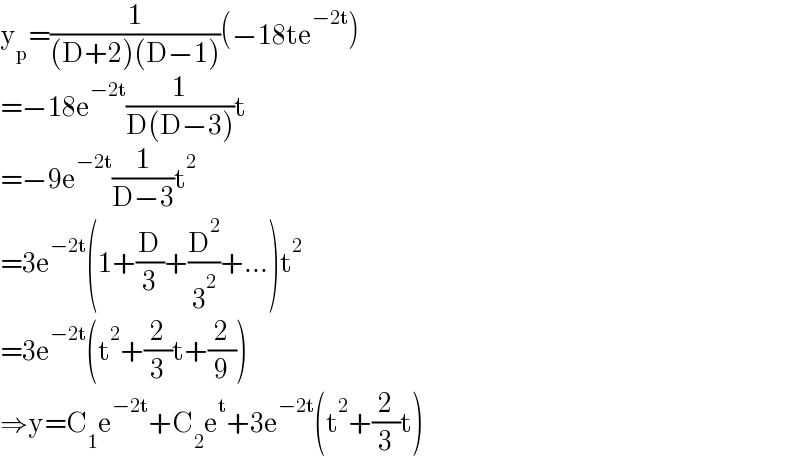
$$\mathrm{y}_{\mathrm{p}} =\frac{\mathrm{1}}{\left(\mathrm{D}+\mathrm{2}\right)\left(\mathrm{D}−\mathrm{1}\right)}\left(−\mathrm{18te}^{−\mathrm{2t}} \right) \\ $$$$=−\mathrm{18e}^{−\mathrm{2t}} \frac{\mathrm{1}}{\mathrm{D}\left(\mathrm{D}−\mathrm{3}\right)}\mathrm{t} \\ $$$$=−\mathrm{9e}^{−\mathrm{2t}} \frac{\mathrm{1}}{\mathrm{D}−\mathrm{3}}\mathrm{t}^{\mathrm{2}} \\ $$$$=\mathrm{3e}^{−\mathrm{2t}} \left(\mathrm{1}+\frac{\mathrm{D}}{\mathrm{3}}+\frac{\mathrm{D}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} }+...\right)\mathrm{t}^{\mathrm{2}} \\ $$$$=\mathrm{3e}^{−\mathrm{2t}} \left(\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{3}}\mathrm{t}+\frac{\mathrm{2}}{\mathrm{9}}\right) \\ $$$$\Rightarrow\mathrm{y}=\mathrm{C}_{\mathrm{1}} \mathrm{e}^{−\mathrm{2t}} +\mathrm{C}_{\mathrm{2}} \mathrm{e}^{\mathrm{t}} +\mathrm{3e}^{−\mathrm{2t}} \left(\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{3}}\mathrm{t}\right) \\ $$
