
Question Number 158228 by Odhiambojr last updated on 01/Nov/21
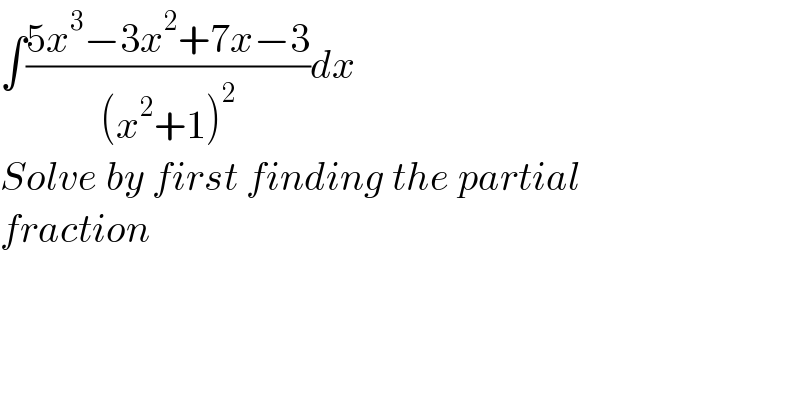
$$\int\frac{\mathrm{5}{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{7}{x}−\mathrm{3}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$${Solve}\:{by}\:{first}\:{finding}\:{the}\:{partial} \\ $$$${fraction} \\ $$
Answered by nimnim last updated on 02/Nov/21
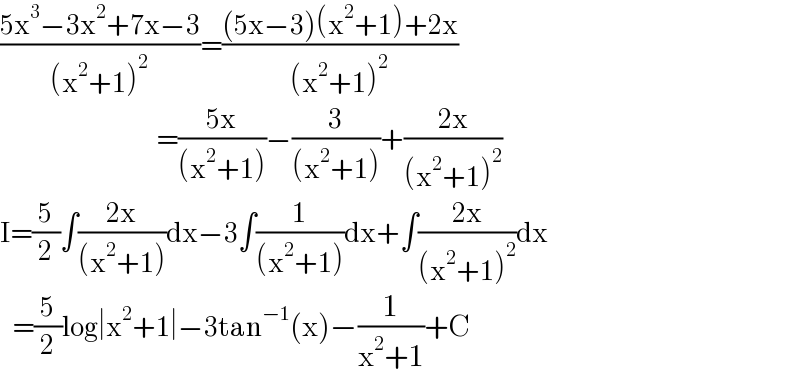
$$\frac{\mathrm{5x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} +\mathrm{7x}−\mathrm{3}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }=\frac{\left(\mathrm{5x}−\mathrm{3}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{5x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\mathrm{3}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}=\frac{\mathrm{5}}{\mathrm{2}}\int\frac{\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dx}−\mathrm{3}\int\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dx}+\int\frac{\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\:=\frac{\mathrm{5}}{\mathrm{2}}\mathrm{log}\mid\mathrm{x}^{\mathrm{2}} +\mathrm{1}\mid−\mathrm{3tan}^{−\mathrm{1}} \left(\mathrm{x}\right)−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}+\mathrm{C} \\ $$
