
Question Number 157870 by Odhiambojr last updated on 29/Oct/21
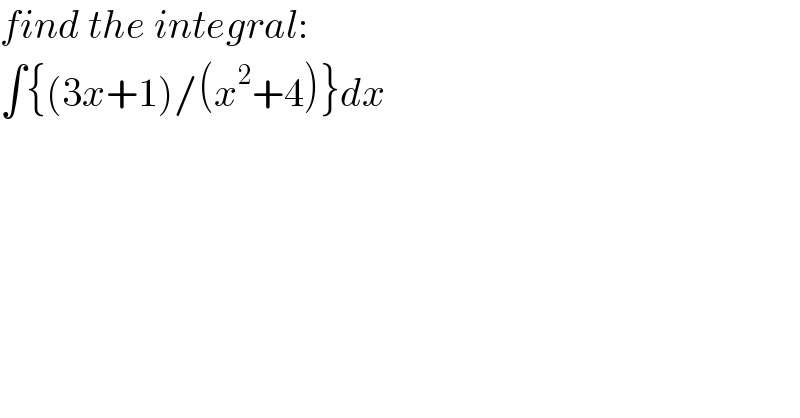
$${find}\:{the}\:{integral}: \\ $$$$\int\left\{\left(\mathrm{3}{x}+\mathrm{1}\right)/\left({x}^{\mathrm{2}} +\mathrm{4}\right)\right\}{dx} \\ $$
Answered by puissant last updated on 29/Oct/21
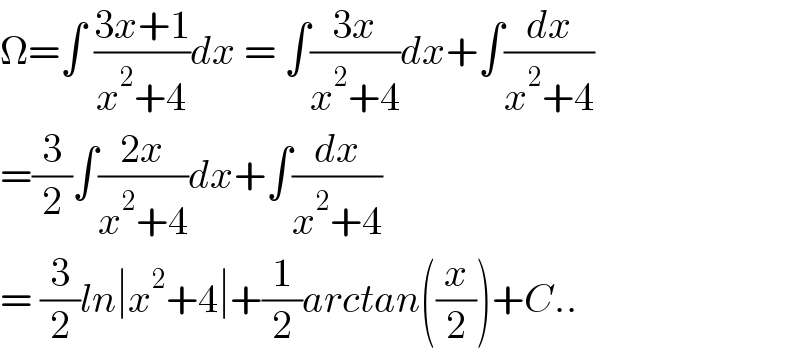
$$\Omega=\int\:\frac{\mathrm{3}{x}+\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{4}}{dx}\:=\:\int\frac{\mathrm{3}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}{dx}+\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{4}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}{dx}+\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{4}} \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} +\mathrm{4}\mid+\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{{x}}{\mathrm{2}}\right)+{C}.. \\ $$
