
Question Number 157839 by gsk2684 last updated on 28/Oct/21
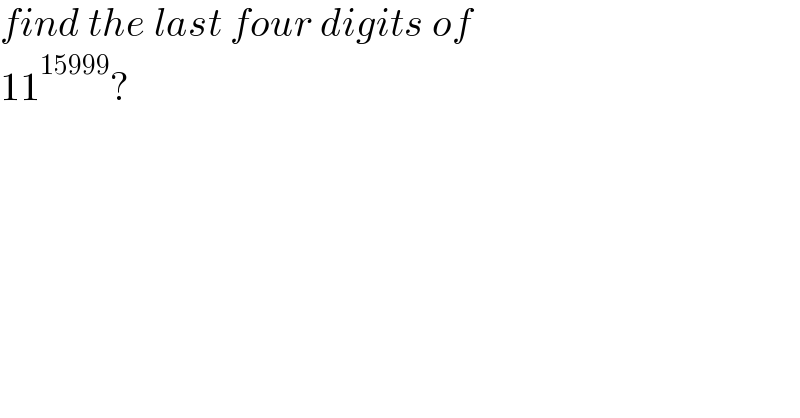
$${find}\:{the}\:{last}\:{four}\:{digits}\:{of}\: \\ $$$$\mathrm{11}^{\mathrm{15999}} ? \\ $$
Answered by Rasheed.Sindhi last updated on 29/Oct/21

$$\mathrm{11}^{\mathrm{15999}} \equiv{x}\left({mod}\:\mathrm{10}^{\mathrm{4}} \right) \\ $$$$\because\:{gcd}\left(\mathrm{11},\mathrm{10}^{\mathrm{4}} \right)=\mathrm{1} \\ $$$$\therefore\:\mathrm{11}^{\phi\left(\mathrm{10}^{\mathrm{4}} \right)} \equiv\mathrm{1}\left({mod}\mathrm{10}^{\mathrm{4}} \right) \\ $$$$\phi\left(\mathrm{10}^{\mathrm{4}} \right)=\mathrm{4000} \\ $$$${Least}\:{number}\:{n}\:{for}\:{which} \\ $$$$\:\:\:\:\mathrm{11}^{{n}} \equiv\mathrm{1}\left({mod}\:\mathrm{10000}\right) \\ $$$${must}\:{be}\:{any}\:{divisor}\:{of}\:\phi\left(\mathrm{10}^{\mathrm{4}} \right)=\mathrm{4000} \\ $$$$ \\ $$$$\mathcal{T}{rying}\:{for}\:{n}=\mathrm{1},\mathrm{2},\mathrm{4},...,\mathrm{500},\mathrm{800},...\mathrm{4000} \\ $$$${we}\:{can}\:{see}\:{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{11}^{\mathrm{500}} \equiv\mathrm{1}\left({mod}\mathrm{10}^{\mathrm{4}} \right) \\ $$$$\because\mathrm{15999}=\mathrm{500}×\mathrm{32}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\mathrm{11}^{\mathrm{500}} \right)^{\mathrm{32}} \equiv\left(\mathrm{1}\right)^{\mathrm{32}} \left({mod}\mathrm{10}^{\mathrm{4}} \right) \\ $$$$\:\:\:\:\:\:\:\mathrm{11}^{\mathrm{16000}} \equiv\mathrm{1}\left({mod}\mathrm{10}^{\mathrm{4}} \right) \\ $$$$\:\:\:\:\:\:\mathrm{11}^{\mathrm{16000}} \equiv\mathrm{1}+\mathrm{10}^{\mathrm{4}} ×\mathrm{10}\left({mod}\mathrm{10}^{\mathrm{4}} \right) \\ $$$$\:\:\:\:\:\:\mathrm{11}^{\mathrm{16000}} \equiv\mathrm{100001}\left({mod}\mathrm{10}^{\mathrm{4}} \right) \\ $$$${Dividing}\:{by}\:\mathrm{11} \\ $$$$\:\:\:\:\:\:\mathrm{11}^{\mathrm{15999}} \equiv\mathrm{9091}\left({mod}\mathrm{10}^{\mathrm{4}} \right) \\ $$$$\:{Last}\:\mathrm{4}\:{digits}\:{of}\:\mathrm{11}^{\mathrm{5999}} \:{are}:\:\mathrm{9091} \\ $$
Commented by gsk2684 last updated on 31/Oct/21

$${thanks}\: \\ $$
