
Question Number 156914 by cortano last updated on 17/Oct/21
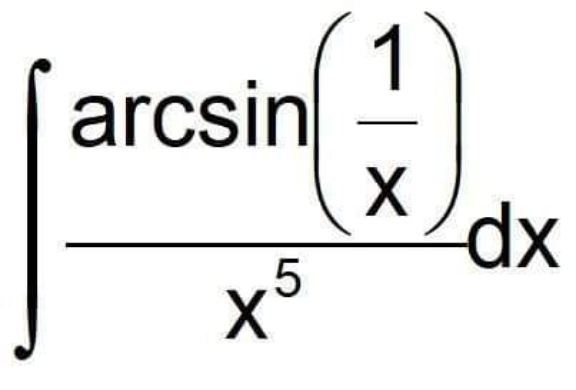
Answered by puissant last updated on 17/Oct/21
![D=∫((arcsin((1/x)))/x^5 )dx ; u=(1/x) → du=−(1/x^2 )dx ⇒ D=−∫ ((u^5 arcsin(u))/u^2 )du=−∫u^3 arcsin(u)du IBP⇒ D=−3[u^2 arcsin(u)]+3∫(u^2 /( (√(1−u^2 ))))du ⇒ D=−3u^2 arcsin(u)−3∫((1−u^2 −1)/( (√(1−u^2 ))))du ⇒ D=−3u^2 arcsin(u)−3∫(√(1−u^2 ))+3∫(1/( (√(1−u^2 ))))du ⇒ D=−3u^2 arcsin(u)−(3/2)[t+(1/2)sin2t]+3arcsin(u)+C ⇒ D=((−3)/x^2 )arcsin((1/x))−(3/2)arcsin((1/x))−(3/2)sin(2arcsin((1/x)))+3arcsin((1/x))+C ∴∵ D=3{((1/2)−(1/x^2 ))arcsin((1/x))−(1/2)sin(2arcsin((1/x)))}+C..](Q156917.png)
$${D}=\int\frac{{arcsin}\left(\frac{\mathrm{1}}{{x}}\right)}{{x}^{\mathrm{5}} }{dx}\:;\:{u}=\frac{\mathrm{1}}{{x}}\:\rightarrow\:{du}=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx} \\ $$$$\Rightarrow\:{D}=−\int\:\frac{{u}^{\mathrm{5}} {arcsin}\left({u}\right)}{{u}^{\mathrm{2}} }{du}=−\int{u}^{\mathrm{3}} {arcsin}\left({u}\right){du} \\ $$$${IBP}\Rightarrow\:{D}=−\mathrm{3}\left[{u}^{\mathrm{2}} {arcsin}\left({u}\right)\right]+\mathrm{3}\int\frac{{u}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}{du} \\ $$$$\Rightarrow\:{D}=−\mathrm{3}{u}^{\mathrm{2}} {arcsin}\left({u}\right)−\mathrm{3}\int\frac{\mathrm{1}−{u}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}{du} \\ $$$$\Rightarrow\:{D}=−\mathrm{3}{u}^{\mathrm{2}} {arcsin}\left({u}\right)−\mathrm{3}\int\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }+\mathrm{3}\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}{du} \\ $$$$\Rightarrow\:{D}=−\mathrm{3}{u}^{\mathrm{2}} {arcsin}\left({u}\right)−\frac{\mathrm{3}}{\mathrm{2}}\left[{t}+\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}{t}\right]+\mathrm{3}{arcsin}\left({u}\right)+{C} \\ $$$$\Rightarrow\:{D}=\frac{−\mathrm{3}}{{x}^{\mathrm{2}} }{arcsin}\left(\frac{\mathrm{1}}{{x}}\right)−\frac{\mathrm{3}}{\mathrm{2}}{arcsin}\left(\frac{\mathrm{1}}{{x}}\right)−\frac{\mathrm{3}}{\mathrm{2}}{sin}\left(\mathrm{2}{arcsin}\left(\frac{\mathrm{1}}{{x}}\right)\right)+\mathrm{3}{arcsin}\left(\frac{\mathrm{1}}{{x}}\right)+{C} \\ $$$$\therefore\because\:{D}=\mathrm{3}\left\{\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){arcsin}\left(\frac{\mathrm{1}}{{x}}\right)−\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{arcsin}\left(\frac{\mathrm{1}}{{x}}\right)\right)\right\}+{C}.. \\ $$
Commented by cortano last updated on 17/Oct/21

$${yes}\:. \\ $$
Answered by cortano last updated on 17/Oct/21

