
Question Number 156513 by cortano last updated on 12/Oct/21
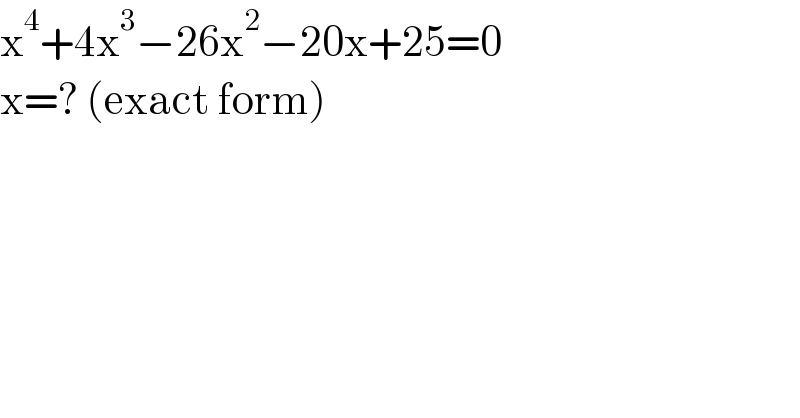
$$\mathrm{x}^{\mathrm{4}} +\mathrm{4x}^{\mathrm{3}} −\mathrm{26x}^{\mathrm{2}} −\mathrm{20x}+\mathrm{25}=\mathrm{0} \\ $$$$\mathrm{x}=?\:\left(\mathrm{exact}\:\mathrm{form}\right) \\ $$
Commented by john_santu last updated on 12/Oct/21

$$\Rightarrow{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{26}−\frac{\mathrm{20}}{{x}}+\frac{\mathrm{25}}{{x}^{\mathrm{2}} }\:=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\frac{\mathrm{5}}{{x}}\right)^{\mathrm{2}} +\mathrm{10}+\mathrm{4}\left({x}−\frac{\mathrm{5}}{{x}}\right)−\mathrm{26}=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\frac{\mathrm{5}}{{x}}\right)^{\mathrm{2}} +\mathrm{4}\left({x}−\frac{\mathrm{5}}{{x}}\right)−\mathrm{16}=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\frac{\mathrm{5}}{{x}}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{20}=\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{{x}−\frac{\mathrm{5}}{{x}}+\mathrm{2}=\mathrm{2}\sqrt{\mathrm{5}}}\\{{x}−\frac{\mathrm{5}}{{x}}+\mathrm{2}=−\mathrm{2}\sqrt{\mathrm{5}}}\end{cases} \\ $$$${case}\left(\mathrm{1}\right)\:{x}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}−\sqrt{\mathrm{5}}\right){x}−\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\pm\sqrt{\mathrm{4}\left(\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}\right)+\mathrm{20}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\pm\mathrm{2}\sqrt{\mathrm{11}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{5}}−\mathrm{1}\pm\sqrt{\mathrm{11}−\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$${case}\left(\mathrm{2}\right)\:{x}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){x}−\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{−\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)\pm\sqrt{\mathrm{4}\left(\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}\right)+\mathrm{20}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{−\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)\pm\mathrm{2}\sqrt{\mathrm{11}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=−\mathrm{1}−\sqrt{\mathrm{5}}\pm\sqrt{\mathrm{11}+\mathrm{2}\sqrt{\mathrm{5}}}\: \\ $$
Commented by Ngeumani last updated on 12/Oct/21

$${is}\:{good} \\ $$
Commented by Tawa11 last updated on 12/Oct/21

$$\mathrm{Weldone} \\ $$
