
Question Number 156136 by SANOGO last updated on 08/Oct/21
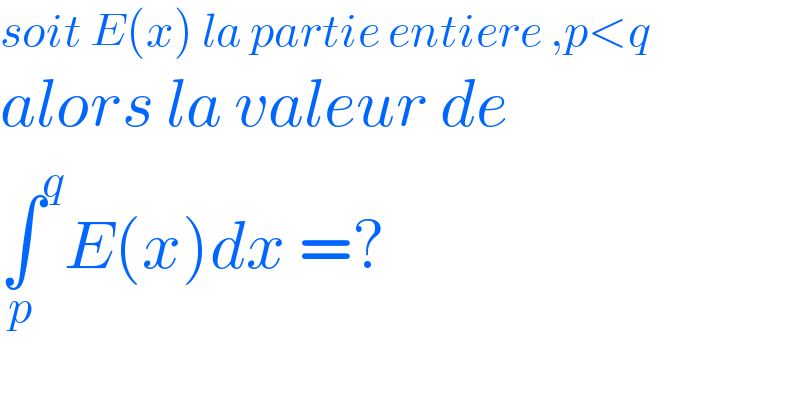
$${soit}\:{E}\left({x}\right)\:{la}\:{partie}\:{entiere}\:,{p}<{q} \\ $$ $${alors}\:{la}\:{valeur}\:{de}\: \\ $$ $$\underset{{p}} {\int}^{{q}} {E}\left({x}\right){dx}\:=? \\ $$
Answered by KONE last updated on 10/Oct/21
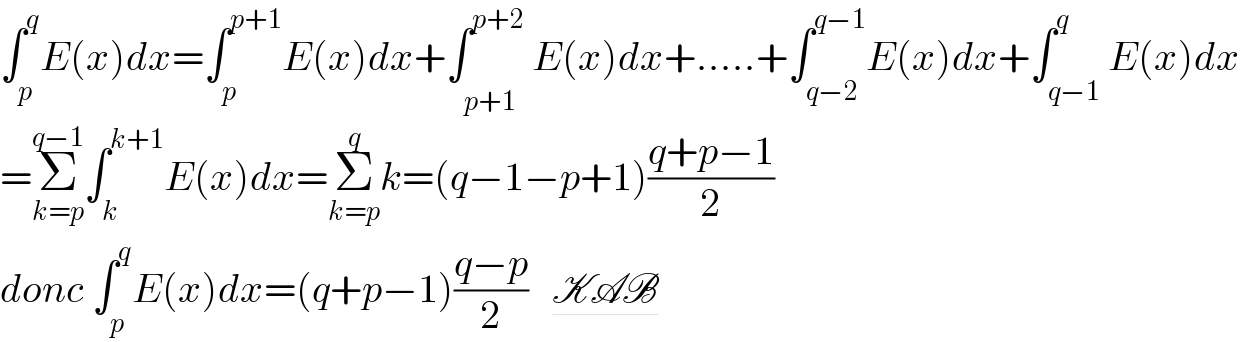
$$\int_{{p}} ^{{q}} {E}\left({x}\right){dx}=\int_{{p}} ^{{p}+\mathrm{1}} {E}\left({x}\right){dx}+\int_{{p}+\mathrm{1}^{} } ^{{p}+\mathrm{2}} {E}\left({x}\right){dx}+.....+\int_{{q}−\mathrm{2}} ^{{q}−\mathrm{1}} {E}\left({x}\right){dx}+\int_{{q}−\mathrm{1}} ^{{q}} {E}\left({x}\right){dx} \\ $$ $$=\underset{{k}={p}} {\overset{{q}−\mathrm{1}} {\sum}}\int_{{k}} ^{{k}+\mathrm{1}} {E}\left({x}\right){dx}=\underset{{k}={p}} {\overset{{q}} {\sum}}{k}=\left({q}−\mathrm{1}−{p}+\mathrm{1}\right)\frac{{q}+{p}−\mathrm{1}}{\mathrm{2}} \\ $$ $${donc}\:\int_{{p}} ^{{q}} {E}\left({x}\right){dx}=\left({q}+{p}−\mathrm{1}\right)\frac{{q}−{p}}{\mathrm{2}}\:\:\:\underline{\mathscr{KAB}} \\ $$
