
Question Number 156126 by VIDDD last updated on 08/Oct/21
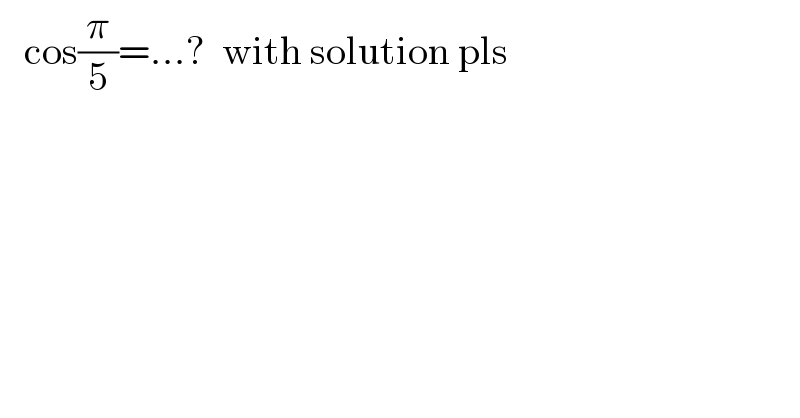
$$\:\:\:\mathrm{cos}\frac{\pi}{\mathrm{5}}=...?\:\:\mathrm{with}\:\mathrm{solution}\:\mathrm{pls} \\ $$
Commented by cortano last updated on 08/Oct/21
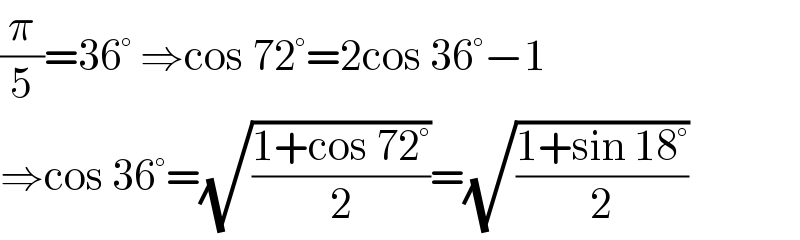
$$\frac{\pi}{\mathrm{5}}=\mathrm{36}°\:\Rightarrow\mathrm{cos}\:\mathrm{72}°=\mathrm{2cos}\:\mathrm{36}°−\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{36}°=\sqrt{\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{72}°}{\mathrm{2}}}=\sqrt{\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{18}°}{\mathrm{2}}} \\ $$
Answered by puissant last updated on 08/Oct/21
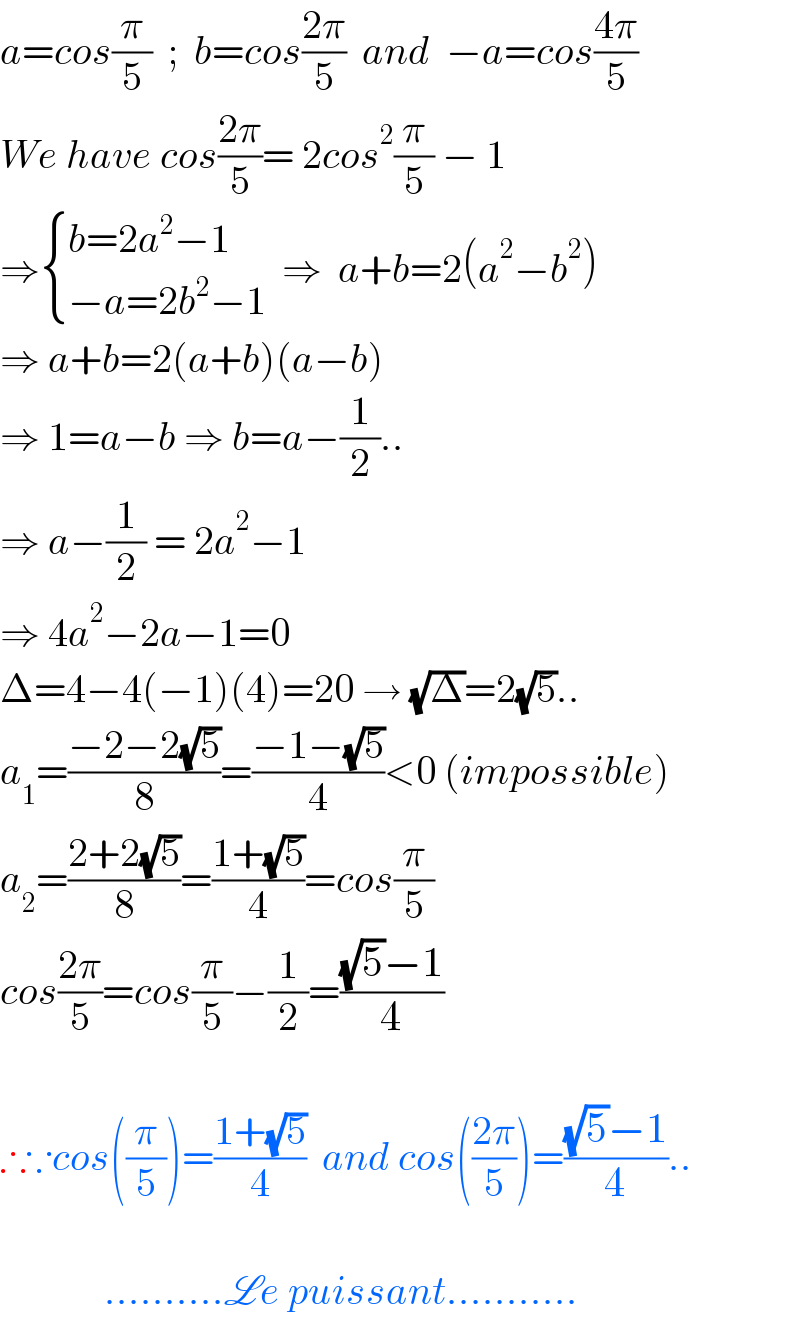
$${a}={cos}\frac{\pi}{\mathrm{5}}\:\:;\:\:{b}={cos}\frac{\mathrm{2}\pi}{\mathrm{5}}\:\:{and}\:\:−{a}={cos}\frac{\mathrm{4}\pi}{\mathrm{5}} \\ $$$${We}\:{have}\:{cos}\frac{\mathrm{2}\pi}{\mathrm{5}}=\:\mathrm{2}{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{5}}\:−\:\mathrm{1} \\ $$$$\Rightarrow\begin{cases}{{b}=\mathrm{2}{a}^{\mathrm{2}} −\mathrm{1}}\\{−{a}=\mathrm{2}{b}^{\mathrm{2}} −\mathrm{1}}\end{cases}\:\:\Rightarrow\:\:{a}+{b}=\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{a}+{b}=\mathrm{2}\left({a}+{b}\right)\left({a}−{b}\right)\: \\ $$$$\Rightarrow\:\mathrm{1}={a}−{b}\:\Rightarrow\:{b}={a}−\frac{\mathrm{1}}{\mathrm{2}}.. \\ $$$$\Rightarrow\:{a}−\frac{\mathrm{1}}{\mathrm{2}}\:=\:\mathrm{2}{a}^{\mathrm{2}} −\mathrm{1}\: \\ $$$$\Rightarrow\:\mathrm{4}{a}^{\mathrm{2}} −\mathrm{2}{a}−\mathrm{1}=\mathrm{0} \\ $$$$\Delta=\mathrm{4}−\mathrm{4}\left(−\mathrm{1}\right)\left(\mathrm{4}\right)=\mathrm{20}\:\rightarrow\:\sqrt{\Delta}=\mathrm{2}\sqrt{\mathrm{5}}.. \\ $$$${a}_{\mathrm{1}} =\frac{−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{8}}=\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}<\mathrm{0}\:\left({impossible}\right) \\ $$$${a}_{\mathrm{2}} =\frac{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{8}}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}={cos}\frac{\pi}{\mathrm{5}} \\ $$$${cos}\frac{\mathrm{2}\pi}{\mathrm{5}}={cos}\frac{\pi}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$$$\therefore\because{cos}\left(\frac{\pi}{\mathrm{5}}\right)=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\:\:{and}\:{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{5}}\right)=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:..........\mathscr{L}{e}\:{puissant}........... \\ $$
Commented by VIDDD last updated on 09/Oct/21

$$\:\:{thanks}\: \\ $$
