
Question Number 155745 by cortano last updated on 04/Oct/21
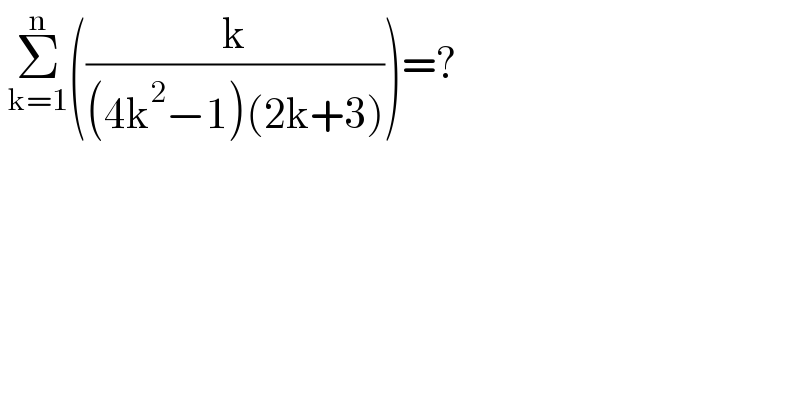
$$\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\frac{\mathrm{k}}{\left(\mathrm{4k}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{2k}+\mathrm{3}\right)}\right)=? \\ $$
Answered by amin96 last updated on 04/Oct/21

$$\underbrace{\frac{{a}}{\mathrm{2}{k}−\underset{\mathrm{4}{k}^{\mathrm{2}} +\mathrm{8}{k}+\mathrm{3}} {\mathrm{1}}}}+\underset{\mathrm{4}{k}^{\mathrm{2}} +\mathrm{4}{k}−\mathrm{3}} {\underbrace{\frac{{b}}{\mathrm{2}{k}+\mathrm{1}}}}+\underset{\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}} {\underbrace{\frac{{c}}{\mathrm{2}{k}+\mathrm{3}}}} \\ $$$$\mathrm{4}{ak}^{\mathrm{2}} +\mathrm{8}{ak}+\mathrm{3}{a}+\mathrm{4}{bk}^{\mathrm{2}} +\mathrm{4}{bk}−\mathrm{3}{b}+\mathrm{4}{ck}^{\mathrm{2}} −{c} \\ $$$$\begin{cases}{\mathrm{4}{a}+\mathrm{4}{b}+\mathrm{4}{c}=\mathrm{0}}\\{\mathrm{8}{a}+\mathrm{4}{b}=\mathrm{1}}\\{\mathrm{3}{a}−\mathrm{3}{b}−{c}=\mathrm{0}\:\:\Rightarrow{a}−{b}=\frac{{c}}{\mathrm{3}}}\end{cases}\: \\ $$$$\mathrm{2}{a}+{b}=\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\mathrm{3}{a}=\frac{{c}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:{a}=\frac{{c}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{12}} \\ $$$${b}={a}−\frac{{c}}{\mathrm{3}}=\frac{{c}−\mathrm{3}{c}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{12}} \\ $$$${b}=\frac{\mathrm{1}}{\mathrm{12}}−\frac{\mathrm{2}{c}}{\mathrm{9}} \\ $$$$\frac{{c}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{12}}−\frac{\mathrm{2}{c}}{\mathrm{9}}+{c}=\mathrm{0}\:\:\:\:\frac{\mathrm{1}}{\mathrm{6}}−\frac{{c}}{\mathrm{9}}+{c}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{6}}=−\frac{\mathrm{8}{c}}{\mathrm{9}}\:\:\:\:\:\:{c}=−\frac{\mathrm{9}}{\mathrm{48}}=−\frac{\mathrm{3}}{\mathrm{16}} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{16}}\:\:{b}=\frac{\mathrm{1}}{\mathrm{8}}\:\:\:{c}=\frac{−\mathrm{3}}{\mathrm{16}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{16}\left(\mathrm{2}{k}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{2}{k}+\mathrm{1}\right)}−\frac{\mathrm{3}}{\mathrm{16}\left(\mathrm{2}{k}+\mathrm{3}\right)}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}+\frac{\mathrm{2}}{\mathrm{2}{k}+\mathrm{1}}−\frac{\mathrm{3}}{\mathrm{2}{k}+\mathrm{3}}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{1}+\underset{{n}−\mathrm{1}} {\underbrace{\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+\ldots+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}}}+\underset{{n}−\mathrm{1}} {\underbrace{\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{7}}+\ldots+}}\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}−\right. \\ $$$$\left.−\frac{\mathrm{3}}{\mathrm{5}}−\frac{\mathrm{3}}{\mathrm{7}}−\frac{\mathrm{3}}{\mathrm{9}}−\ldots−\frac{\mathrm{3}}{\mathrm{2}{n}+\mathrm{3}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{1}+\mathrm{1}+\frac{\mathrm{3}}{\mathrm{5}}+\frac{\mathrm{3}}{\mathrm{7}}+\frac{\mathrm{3}}{\mathrm{9}}+\ldots+\frac{\mathrm{3}}{\mathrm{2}{n}−\mathrm{1}}+\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}−\frac{\mathrm{3}}{\mathrm{5}}−\frac{\mathrm{7}}{\mathrm{3}}−\frac{\mathrm{9}}{\mathrm{3}}−\ldots−\frac{\mathrm{3}}{\mathrm{2}{n}+\mathrm{3}}\right)= \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{2}+\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}−\frac{\mathrm{3}}{\mathrm{2}{n}+\mathrm{1}}−\frac{\mathrm{3}}{\mathrm{2}{n}+\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}−\frac{\mathrm{3}}{\mathrm{2}{n}+\mathrm{3}}\right)= \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\left(\frac{\mathrm{2}\left(\mathrm{4}{n}^{\mathrm{2}} +\mathrm{8}{n}+\mathrm{3}\right)−\mathrm{2}{n}−\mathrm{3}−\mathrm{6}{n}−\mathrm{3}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left(\frac{\mathrm{8}{n}^{\mathrm{2}} +\mathrm{16}{n}+\mathrm{6}−\mathrm{8}{n}−\mathrm{6}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)}\right)=\frac{\mathrm{1}}{\mathrm{16}}\left(\frac{\mathrm{8}{n}^{\mathrm{2}} +\mathrm{8}{n}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)}\right)= \\ $$$$=\frac{{n}^{\mathrm{2}} +{n}}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)} \\ $$$${MATH}.{AMIN}\: \\ $$$$ \\ $$
Commented by Tawa11 last updated on 04/Oct/21

$$\mathrm{Weldone}\:\mathrm{sir} \\ $$
Commented by cortano last updated on 05/Oct/21

$$\mathrm{nice} \\ $$$$ \\ $$
Answered by TheSupreme last updated on 04/Oct/21
![(A/(2k−1))+(B/(2k+1))+(C/(2k+3))=((A(2k+1)(2k+3)+B(2k−1)(2k+3)+C(4k^2 −1))/D) { ((A+B+C=0)),((2A+B=(1/4))),((3A−3B−C=0)) :} A=−C−B −2C−2B+B=(1/4)→ B=2C−(1/4) −3C−3(2C−(1/4))−3(2C−(1/4))−C=0 −3C−6C+(3/4)−6C+(3/4)−C=0 −15C=−(6/4) → C=(1/(10)) B=(1/5)−(1/4)=−(1/(20)) A=−(1/(20)) Σ=(1/(10))[−(1/2)(1/(2k+1))−(1/2)(1/(2k−1))+(1/(2k+3))] =(1/(10))[−(1/2)( (1/1)+(1/3)+(1/5)+...)−(1/2)((1/3)+(1/5)+...)+(1/5)] =(1/(10))[−(1/2)−(1/2)((1/3))]=−(1/(15))](Q155754.png)
$$\frac{{A}}{\mathrm{2}{k}−\mathrm{1}}+\frac{{B}}{\mathrm{2}{k}+\mathrm{1}}+\frac{{C}}{\mathrm{2}{k}+\mathrm{3}}=\frac{{A}\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)+{B}\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)+{C}\left(\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}\right)}{{D}} \\ $$$$\begin{cases}{{A}+{B}+{C}=\mathrm{0}}\\{\mathrm{2}{A}+{B}=\frac{\mathrm{1}}{\mathrm{4}}}\\{\mathrm{3}{A}−\mathrm{3}{B}−{C}=\mathrm{0}}\end{cases} \\ $$$${A}=−{C}−{B} \\ $$$$−\mathrm{2}{C}−\mathrm{2}{B}+{B}=\frac{\mathrm{1}}{\mathrm{4}}\rightarrow\:{B}=\mathrm{2}{C}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$−\mathrm{3}{C}−\mathrm{3}\left(\mathrm{2}{C}−\frac{\mathrm{1}}{\mathrm{4}}\right)−\mathrm{3}\left(\mathrm{2}{C}−\frac{\mathrm{1}}{\mathrm{4}}\right)−{C}=\mathrm{0} \\ $$$$−\mathrm{3}{C}−\mathrm{6}{C}+\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{6}{C}+\frac{\mathrm{3}}{\mathrm{4}}−{C}=\mathrm{0} \\ $$$$−\mathrm{15}{C}=−\frac{\mathrm{6}}{\mathrm{4}}\:\rightarrow\:{C}=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$${B}=\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{4}}=−\frac{\mathrm{1}}{\mathrm{20}} \\ $$$${A}=−\frac{\mathrm{1}}{\mathrm{20}} \\ $$$$\Sigma=\frac{\mathrm{1}}{\mathrm{10}}\left[−\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{3}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\left[−\frac{\mathrm{1}}{\mathrm{2}}\left(\:\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+...\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+...\right)+\frac{\mathrm{1}}{\mathrm{5}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\left[−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right]=−\frac{\mathrm{1}}{\mathrm{15}} \\ $$$$ \\ $$
Commented by amin96 last updated on 04/Oct/21
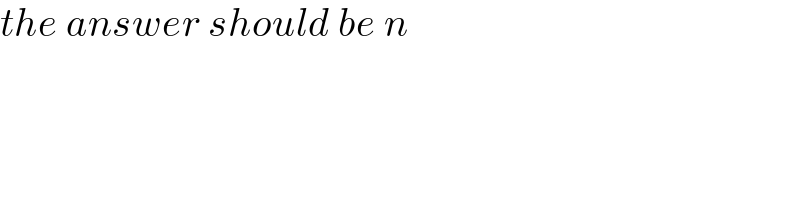
$${the}\:{answer}\:{should}\:{be}\:{n} \\ $$
