Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 155547 by mathdanisur last updated on 02/Oct/21

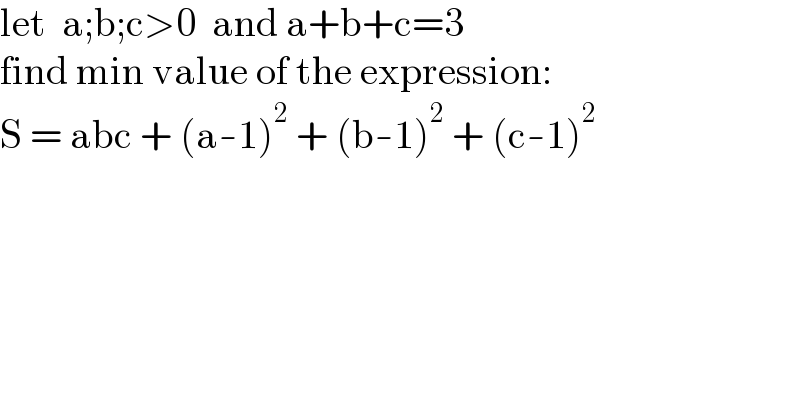
let a;b;c>0 and a+b+c=3 find min value of the expression: S = abc + (a-1)^2 + (b-1)^2 + (c-1)^2

$$\mathrm{let}\:\:\mathrm{a};\mathrm{b};\mathrm{c}>\mathrm{0}\:\:\mathrm{and}\:\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{3} \\ $$ $$\mathrm{find}\:\mathrm{min}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{expression}: \\ $$ $$\mathrm{S}\:=\:\mathrm{abc}\:+\:\left(\mathrm{a}-\mathrm{1}\right)^{\mathrm{2}} \:+\:\left(\mathrm{b}-\mathrm{1}\right)^{\mathrm{2}} \:+\:\left(\mathrm{c}-\mathrm{1}\right)^{\mathrm{2}} \\ $$

Answered by ghimisi last updated on 02/Oct/21

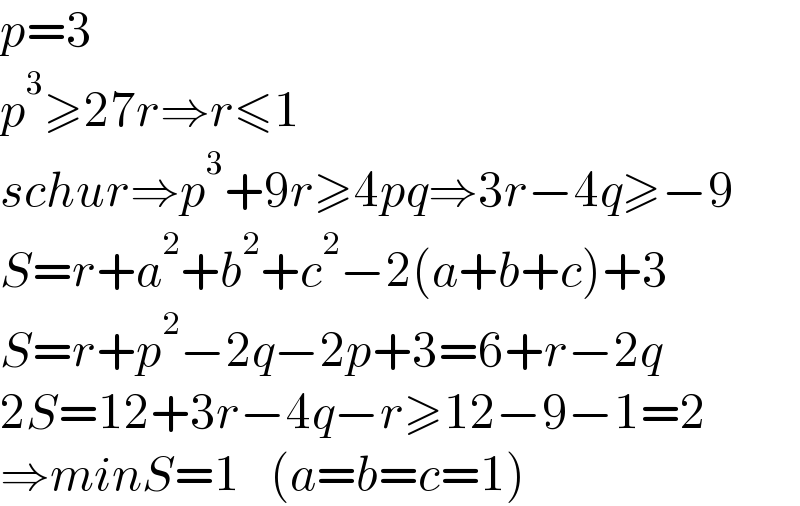
p=3 p^3 ≥27r⇒r≤1 schur⇒p^3 +9r≥4pq⇒3r−4q≥−9 S=r+a^2 +b^2 +c^2 −2(a+b+c)+3 S=r+p^2 −2q−2p+3=6+r−2q 2S=12+3r−4q−r≥12−9−1=2 ⇒minS=1 (a=b=c=1)

$${p}=\mathrm{3} \\ $$ $${p}^{\mathrm{3}} \geqslant\mathrm{27}{r}\Rightarrow{r}\leqslant\mathrm{1} \\ $$ $${schur}\Rightarrow{p}^{\mathrm{3}} +\mathrm{9}{r}\geqslant\mathrm{4}{pq}\Rightarrow\mathrm{3}{r}−\mathrm{4}{q}\geqslant−\mathrm{9} \\ $$ $${S}={r}+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}\left({a}+{b}+{c}\right)+\mathrm{3} \\ $$ $${S}={r}+{p}^{\mathrm{2}} −\mathrm{2}{q}−\mathrm{2}{p}+\mathrm{3}=\mathrm{6}+{r}−\mathrm{2}{q} \\ $$ $$\mathrm{2}{S}=\mathrm{12}+\mathrm{3}{r}−\mathrm{4}{q}−{r}\geqslant\mathrm{12}−\mathrm{9}−\mathrm{1}=\mathrm{2} \\ $$ $$\Rightarrow{minS}=\mathrm{1}\:\:\:\left({a}={b}={c}=\mathrm{1}\right) \\ $$

Commented bymathdanisur last updated on 02/Oct/21

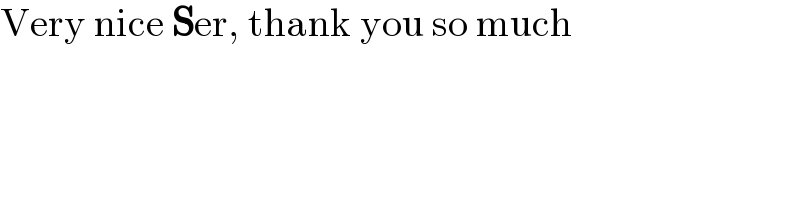
Very nice Ser, thank you so much

$$\mathrm{Very}\:\mathrm{nice}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com