
Question Number 155400 by TVTA last updated on 30/Sep/21
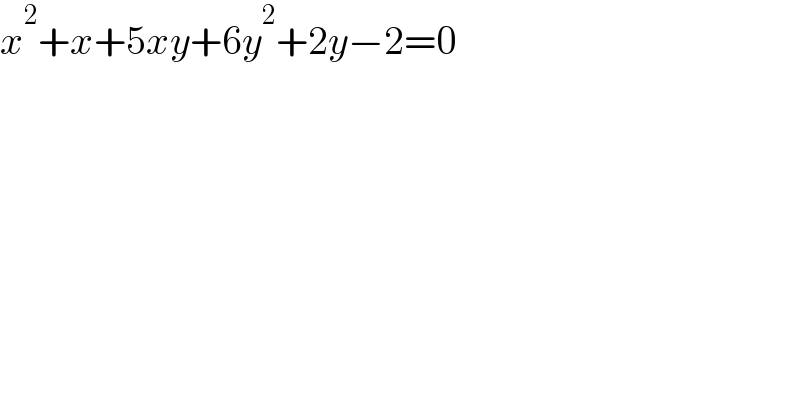
$${x}^{\mathrm{2}} +{x}+\mathrm{5}{xy}+\mathrm{6}{y}^{\mathrm{2}} +\mathrm{2}{y}−\mathrm{2}=\mathrm{0} \\ $$
Commented by MJS_new last updated on 30/Sep/21
![hyperbola with center [(2),((−1)) ] and axes a=2(√(−7+5(√2))) b=2(√(7+5(√2))) rotated by ((3π)/8)=67.5° the transformed equation is (x^2 /(−28+20(√2)))−(y^2 /(28+20(√2)))=1](Q155411.png)
$$\mathrm{hyperbola}\:\mathrm{with}\:\mathrm{center}\:\begin{bmatrix}{\mathrm{2}}\\{−\mathrm{1}}\end{bmatrix}\:\mathrm{and}\:\mathrm{axes} \\ $$$${a}=\mathrm{2}\sqrt{−\mathrm{7}+\mathrm{5}\sqrt{\mathrm{2}}} \\ $$$${b}=\mathrm{2}\sqrt{\mathrm{7}+\mathrm{5}\sqrt{\mathrm{2}}} \\ $$$$\mathrm{rotated}\:\mathrm{by}\:\frac{\mathrm{3}\pi}{\mathrm{8}}=\mathrm{67}.\mathrm{5}° \\ $$$$\mathrm{the}\:\mathrm{transformed}\:\mathrm{equation}\:\mathrm{is} \\ $$$$\frac{{x}^{\mathrm{2}} }{−\mathrm{28}+\mathrm{20}\sqrt{\mathrm{2}}}−\frac{{y}^{\mathrm{2}} }{\mathrm{28}+\mathrm{20}\sqrt{\mathrm{2}}}=\mathrm{1} \\ $$
