
Question Number 155384 by aliyn last updated on 29/Sep/21
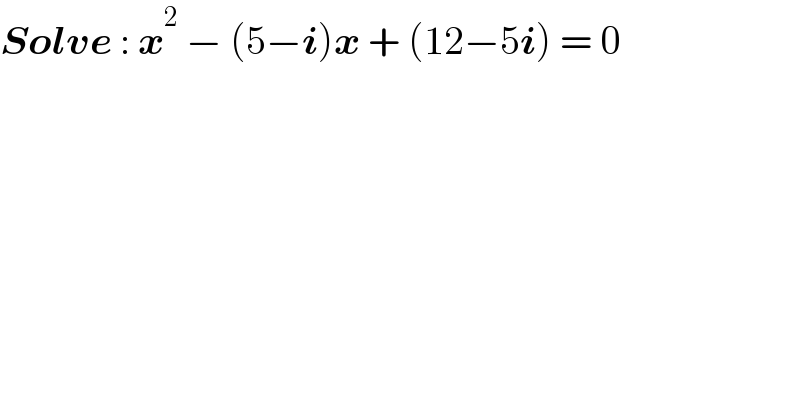
$$\boldsymbol{{Solve}}\::\:\boldsymbol{{x}}^{\mathrm{2}} \:−\:\left(\mathrm{5}−\boldsymbol{{i}}\right)\boldsymbol{{x}}\:+\:\left(\mathrm{12}−\mathrm{5}\boldsymbol{{i}}\right)\:=\:\mathrm{0} \\ $$
Commented by aliyn last updated on 29/Sep/21

$$???? \\ $$
Answered by puissant last updated on 30/Sep/21
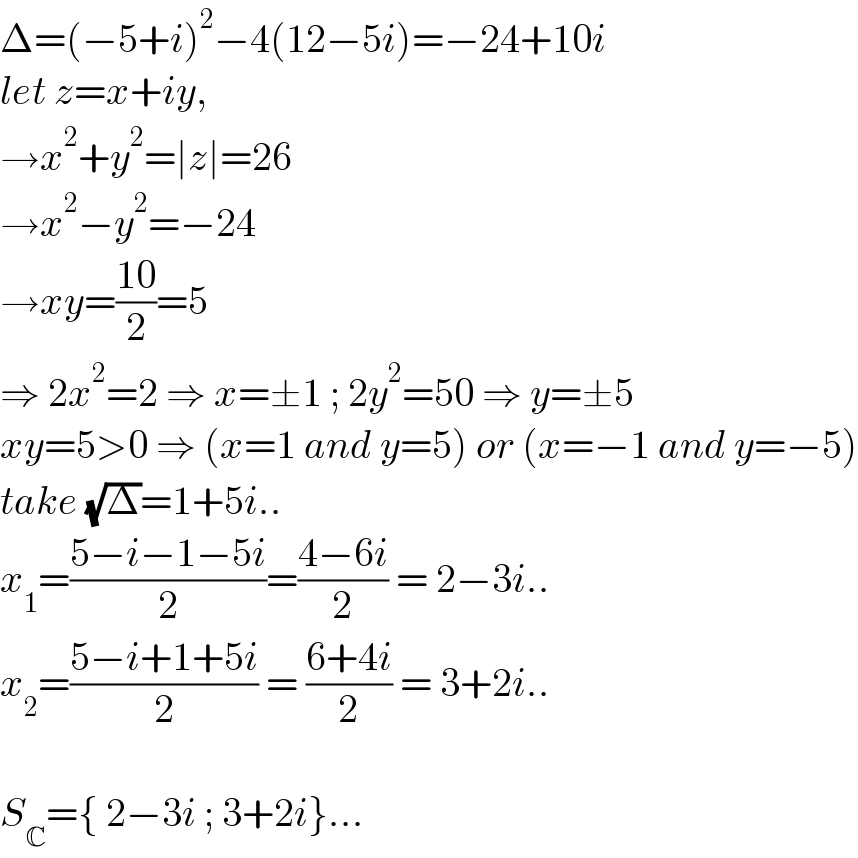
$$\Delta=\left(−\mathrm{5}+{i}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{12}−\mathrm{5}{i}\right)=−\mathrm{24}+\mathrm{10}{i} \\ $$$${let}\:{z}={x}+{iy}, \\ $$$$\rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mid{z}\mid=\mathrm{26} \\ $$$$\rightarrow{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =−\mathrm{24} \\ $$$$\rightarrow{xy}=\frac{\mathrm{10}}{\mathrm{2}}=\mathrm{5} \\ $$$$\Rightarrow\:\mathrm{2}{x}^{\mathrm{2}} =\mathrm{2}\:\Rightarrow\:{x}=\pm\mathrm{1}\:;\:\mathrm{2}{y}^{\mathrm{2}} =\mathrm{50}\:\Rightarrow\:{y}=\pm\mathrm{5} \\ $$$${xy}=\mathrm{5}>\mathrm{0}\:\Rightarrow\:\left({x}=\mathrm{1}\:{and}\:{y}=\mathrm{5}\right)\:{or}\:\left({x}=−\mathrm{1}\:{and}\:{y}=−\mathrm{5}\right) \\ $$$${take}\:\sqrt{\Delta}=\mathrm{1}+\mathrm{5}{i}.. \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{5}−{i}−\mathrm{1}−\mathrm{5}{i}}{\mathrm{2}}=\frac{\mathrm{4}−\mathrm{6}{i}}{\mathrm{2}}\:=\:\mathrm{2}−\mathrm{3}{i}.. \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{5}−{i}+\mathrm{1}+\mathrm{5}{i}}{\mathrm{2}}\:=\:\frac{\mathrm{6}+\mathrm{4}{i}}{\mathrm{2}}\:=\:\mathrm{3}+\mathrm{2}{i}.. \\ $$$$ \\ $$$${S}_{\mathbb{C}} =\left\{\:\mathrm{2}−\mathrm{3}{i}\:;\:\mathrm{3}+\mathrm{2}{i}\right\}... \\ $$
Answered by MJS_new last updated on 30/Sep/21
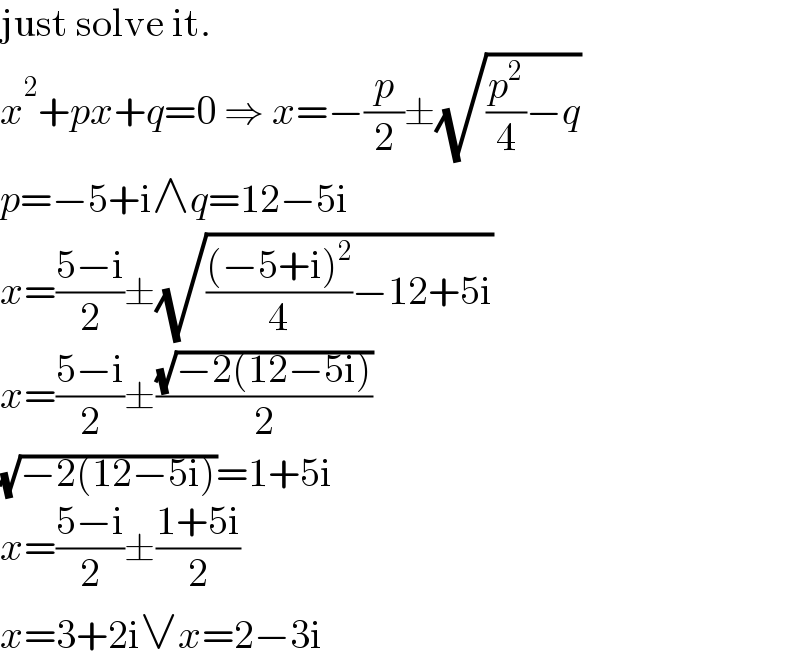
$$\mathrm{just}\:\mathrm{solve}\:\mathrm{it}. \\ $$$${x}^{\mathrm{2}} +{px}+{q}=\mathrm{0}\:\Rightarrow\:{x}=−\frac{{p}}{\mathrm{2}}\pm\sqrt{\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}} \\ $$$${p}=−\mathrm{5}+\mathrm{i}\wedge{q}=\mathrm{12}−\mathrm{5i} \\ $$$${x}=\frac{\mathrm{5}−\mathrm{i}}{\mathrm{2}}\pm\sqrt{\frac{\left(−\mathrm{5}+\mathrm{i}\right)^{\mathrm{2}} }{\mathrm{4}}−\mathrm{12}+\mathrm{5i}} \\ $$$${x}=\frac{\mathrm{5}−\mathrm{i}}{\mathrm{2}}\pm\frac{\sqrt{−\mathrm{2}\left(\mathrm{12}−\mathrm{5i}\right)}}{\mathrm{2}} \\ $$$$\sqrt{−\mathrm{2}\left(\mathrm{12}−\mathrm{5i}\right)}=\mathrm{1}+\mathrm{5i} \\ $$$${x}=\frac{\mathrm{5}−\mathrm{i}}{\mathrm{2}}\pm\frac{\mathrm{1}+\mathrm{5i}}{\mathrm{2}} \\ $$$${x}=\mathrm{3}+\mathrm{2i}\vee{x}=\mathrm{2}−\mathrm{3i} \\ $$
Commented by puissant last updated on 30/Sep/21
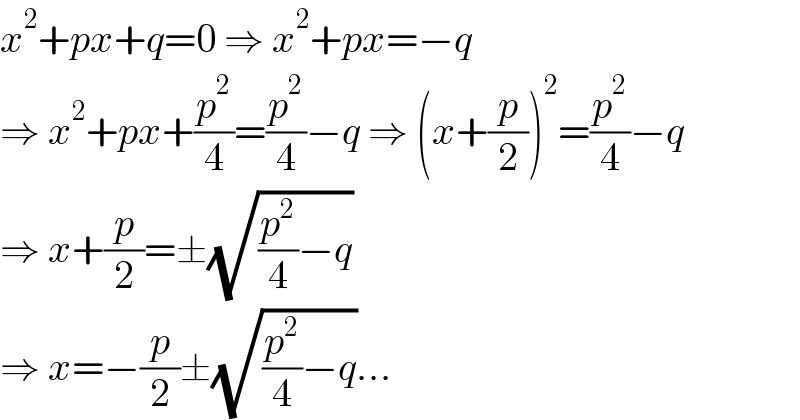
$${x}^{\mathrm{2}} +{px}+{q}=\mathrm{0}\:\Rightarrow\:{x}^{\mathrm{2}} +{px}=−{q} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} +{px}+\frac{{p}^{\mathrm{2}} }{\mathrm{4}}=\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}\:\Rightarrow\:\left({x}+\frac{{p}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q} \\ $$$$\Rightarrow\:{x}+\frac{{p}}{\mathrm{2}}=\pm\sqrt{\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}} \\ $$$$\Rightarrow\:{x}=−\frac{{p}}{\mathrm{2}}\pm\sqrt{\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}}... \\ $$
