
Question Number 155382 by MathsFan last updated on 29/Sep/21
Answered by puissant last updated on 29/Sep/21
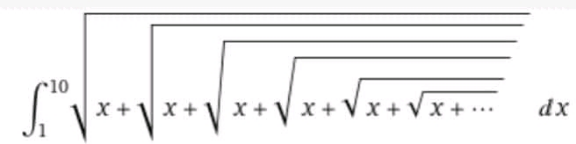
![Q=∫_0 ^(10) (√(x+(√(x+(√(x+(√(x+...))))))))dx u=(√(x+(√(x+(√(x+(√(x+....))))))))→u^2 =x+(√(x+(√(x+(√(x+....)))))) ⇒ u^2 −u=x ⇒ u−u+(1/4)=x+(1/4) ⇒ (u−(1/2))^2 =x+(1/4) ⇒ u=(1/2)+(√((4x+1)/4)) Q=∫_0 ^(10) ((1/2)+(1/2)(√(4x+1)))dx=(1/2)∫_0 ^(10) (1+(√(4x+1)))dx =(1/2)[x+(2/3)×(1/4)(√((4x+1)^3 ))]_0 ^(10) =(1/2)[x+(1/6)(√((4x+1)^3 ))]_0 ^(10) =(1/2)[(10+((√(68921))/6))−(0+(1/6))] ∴ ∵ Q= (1/(12))(59+2(√(68921))).. ..............Le puissant...............](Q155387.png)
$${Q}=\int_{\mathrm{0}} ^{\mathrm{10}} \sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+...}}}}{dx} \\ $$$${u}=\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+....}}}}\rightarrow{u}^{\mathrm{2}} ={x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+....}}} \\ $$$$\Rightarrow\:{u}^{\mathrm{2}} −{u}={x}\:\Rightarrow\:{u}−{u}+\frac{\mathrm{1}}{\mathrm{4}}={x}+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\:\left({u}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} ={x}+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:{u}=\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\frac{\mathrm{4}{x}+\mathrm{1}}{\mathrm{4}}} \\ $$$${Q}=\int_{\mathrm{0}} ^{\mathrm{10}} \left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{4}{x}+\mathrm{1}}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{10}} \left(\mathrm{1}+\sqrt{\mathrm{4}{x}+\mathrm{1}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{x}+\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\left(\mathrm{4}{x}+\mathrm{1}\right)^{\mathrm{3}} }\right]_{\mathrm{0}} ^{\mathrm{10}} =\frac{\mathrm{1}}{\mathrm{2}}\left[{x}+\frac{\mathrm{1}}{\mathrm{6}}\sqrt{\left(\mathrm{4}{x}+\mathrm{1}\right)^{\mathrm{3}} }\right]_{\mathrm{0}} ^{\mathrm{10}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\mathrm{10}+\frac{\sqrt{\mathrm{68921}}}{\mathrm{6}}\right)−\left(\mathrm{0}+\frac{\mathrm{1}}{\mathrm{6}}\right)\right] \\ $$$$ \\ $$$$\:\:\:\:\:\:\therefore\:\because\:\:\:\:\:\:\:{Q}=\:\frac{\mathrm{1}}{\mathrm{12}}\left(\mathrm{59}+\mathrm{2}\sqrt{\mathrm{68921}}\right).. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:..............\mathscr{L}{e}\:{puissant}............... \\ $$$$ \\ $$
Commented by SANOGO last updated on 30/Sep/21
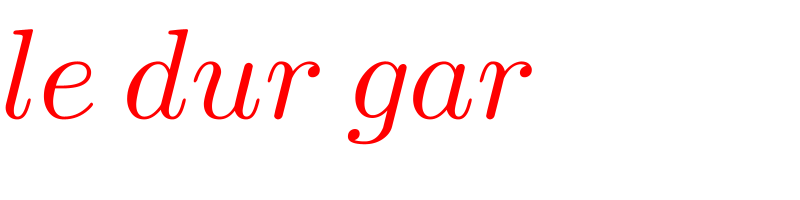
$${le}\:{dur}\:{gar} \\ $$
Commented by MathsFan last updated on 30/Sep/21

$${correct}\:{sir} \\ $$
Commented by peter frank last updated on 01/Oct/21

$$\mathrm{good} \\ $$
