
Question Number 155377 by mathdanisur last updated on 29/Sep/21
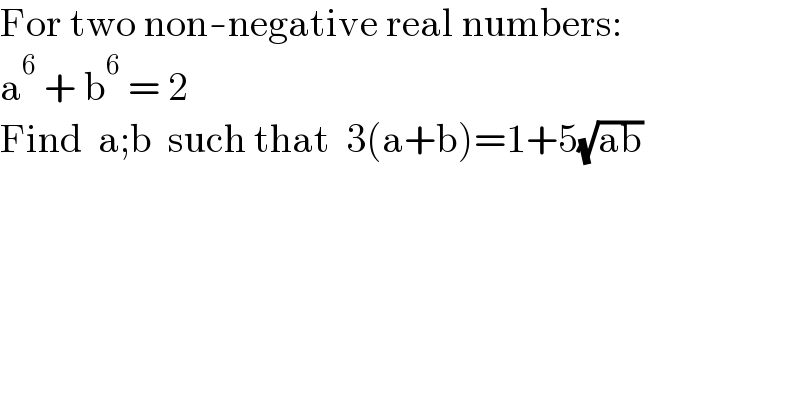
$$\mathrm{For}\:\mathrm{two}\:\mathrm{non}-\mathrm{negative}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\mathrm{a}^{\mathrm{6}} \:+\:\mathrm{b}^{\mathrm{6}} \:=\:\mathrm{2} \\ $$$$\mathrm{Find}\:\:\mathrm{a};\mathrm{b}\:\:\mathrm{such}\:\mathrm{that}\:\:\mathrm{3}\left(\mathrm{a}+\mathrm{b}\right)=\mathrm{1}+\mathrm{5}\sqrt{\mathrm{ab}} \\ $$
Answered by MJS_new last updated on 30/Sep/21

$$\mathrm{the}\:\mathrm{only}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{is}\:{a}={b}=\mathrm{1} \\ $$
Commented by mathdanisur last updated on 30/Sep/21
$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{how}\:\mathrm{if}\:\mathrm{possible} \\ $$
Answered by MJS_new last updated on 30/Sep/21

$$\mathrm{3}\left({a}+{b}\right)=\mathrm{1}+\mathrm{5}\sqrt{{ab}} \\ $$$$\mathrm{let}\:{a}={u}−{v}\wedge{b}={u}+{v} \\ $$$$\mathrm{6}{u}=\mathrm{1}+\mathrm{5}\sqrt{{u}^{\mathrm{2}} −{v}^{\mathrm{2}} }\:\Rightarrow\:{v}^{\mathrm{2}} =−\frac{\mathrm{11}{u}^{\mathrm{2}} −\mathrm{12}{u}+\mathrm{1}}{\mathrm{25}} \\ $$$${a}^{\mathrm{6}} +{b}^{\mathrm{6}} −\mathrm{2}=\mathrm{0} \\ $$$${u}^{\mathrm{6}} +\mathrm{15}{u}^{\mathrm{4}} {v}^{\mathrm{2}} +\mathrm{15}{u}^{\mathrm{2}} {v}^{\mathrm{4}} +{v}^{\mathrm{6}} −\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{inserting}\:\&\:\mathrm{transforming} \\ $$$${u}^{\mathrm{6}} −\frac{\mathrm{279}}{\mathrm{679}}{u}^{\mathrm{5}} −\frac{\mathrm{2985}}{\mathrm{2716}}{u}^{\mathrm{4}} +\frac{\mathrm{405}}{\mathrm{2716}}{u}^{\mathrm{3}} +\frac{\mathrm{45}}{\mathrm{21728}}{u}^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{10864}}{u}+\frac{\mathrm{7813}}{\mathrm{21728}}=\mathrm{0} \\ $$$$\left({u}−\mathrm{1}\right)^{\mathrm{2}} \left({u}^{\mathrm{4}} +\frac{\mathrm{1079}}{\mathrm{679}}{u}^{\mathrm{3}} +\frac{\mathrm{2931}}{\mathrm{2716}}{u}^{\mathrm{2}} +\frac{\mathrm{1951}}{\mathrm{2716}}{u}+\frac{\mathrm{7813}}{\mathrm{21728}}\right)=\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{has}\:\mathrm{no}\:\mathrm{other}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{than} \\ $$$${u}=\mathrm{1} \\ $$$$\Rightarrow \\ $$$${v}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${a}={b}=\mathrm{1} \\ $$
Commented by mathdanisur last updated on 30/Sep/21

$$\mathrm{Very}\:\mathrm{impressive}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{thank}\:\mathrm{you} \\ $$
