
Question Number 155372 by mathdanisur last updated on 29/Sep/21

Commented by Rasheed.Sindhi last updated on 30/Sep/21
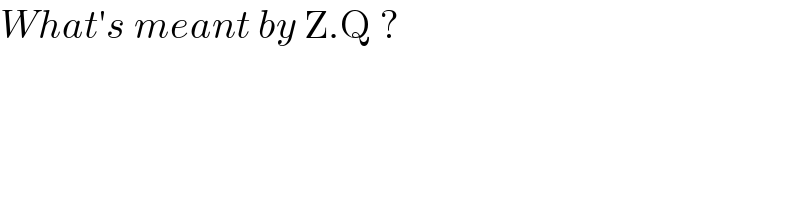
$${What}'{s}\:{meant}\:{by}\:\mathrm{Z}.\mathrm{Q}\:? \\ $$
Commented by mathdanisur last updated on 30/Sep/21
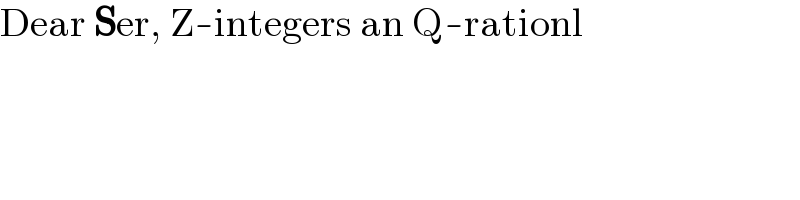
$$\mathrm{Dear}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{Z}-\mathrm{integers}\:\mathrm{an}\:\mathrm{Q}-\mathrm{rationl} \\ $$
Commented by Rasheed.Sindhi last updated on 01/Oct/21
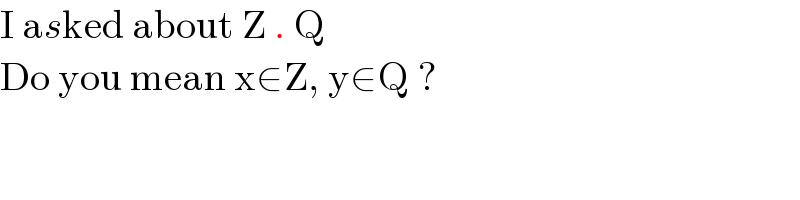
$$\mathrm{I}\:\mathrm{a}{s}\mathrm{ked}\:\mathrm{about}\:\mathrm{Z}\:.\:\mathrm{Q} \\ $$$$\mathrm{Do}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{x}\in\mathrm{Z},\:\mathrm{y}\in\mathrm{Q}\:? \\ $$
Commented by mathdanisur last updated on 30/Sep/21

$$\mathrm{Dear}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{yes} \\ $$
Answered by Rasheed.Sindhi last updated on 30/Sep/21
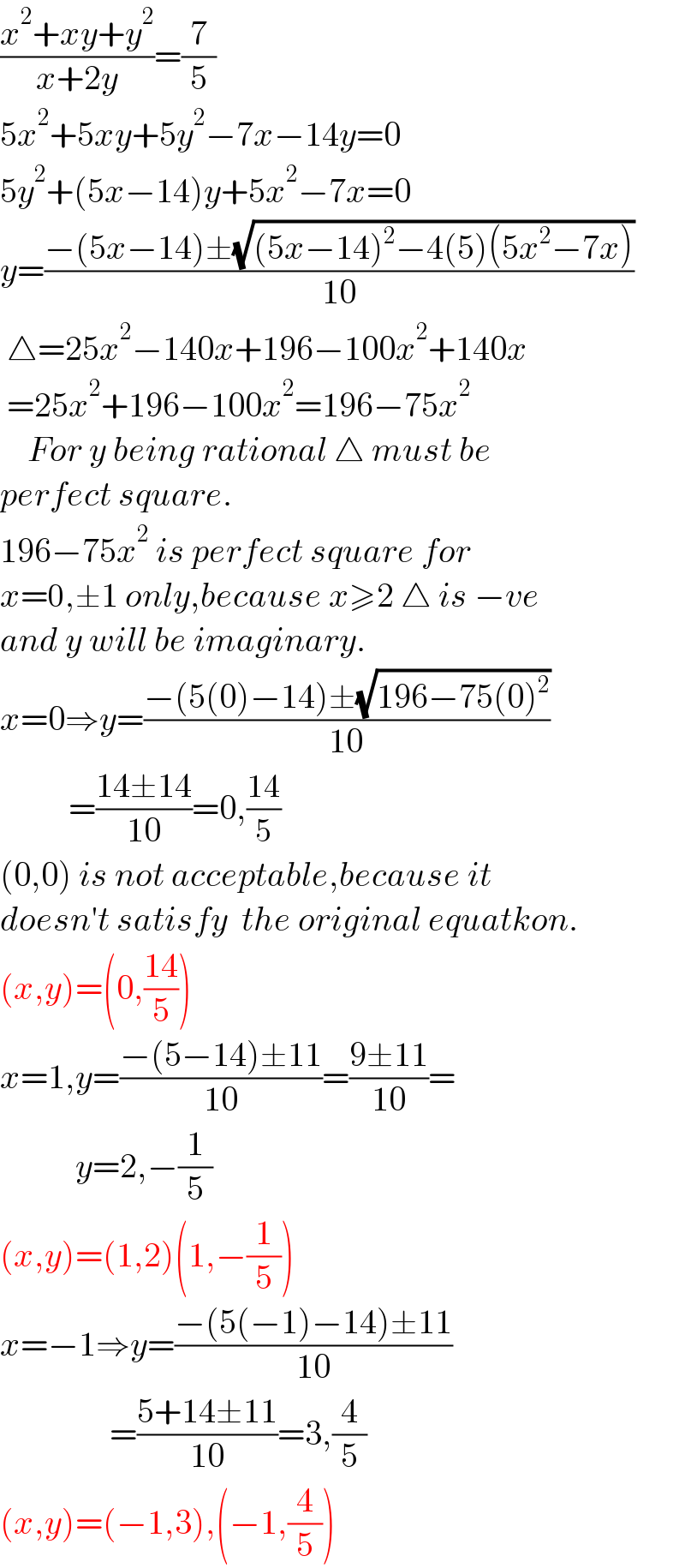
$$\frac{{x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} }{{x}+\mathrm{2}{y}}=\frac{\mathrm{7}}{\mathrm{5}} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{5}{xy}+\mathrm{5}{y}^{\mathrm{2}} −\mathrm{7}{x}−\mathrm{14}{y}=\mathrm{0} \\ $$$$\mathrm{5}{y}^{\mathrm{2}} +\left(\mathrm{5}{x}−\mathrm{14}\right){y}+\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}=\mathrm{0} \\ $$$${y}=\frac{−\left(\mathrm{5}{x}−\mathrm{14}\right)\pm\sqrt{\left(\mathrm{5}{x}−\mathrm{14}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{5}\right)\left(\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}\right)}}{\mathrm{10}} \\ $$$$\:\bigtriangleup=\mathrm{25}{x}^{\mathrm{2}} −\mathrm{140}{x}+\mathrm{196}−\mathrm{100}{x}^{\mathrm{2}} +\mathrm{140}{x} \\ $$$$\:=\mathrm{25}{x}^{\mathrm{2}} +\mathrm{196}−\mathrm{100}{x}^{\mathrm{2}} =\mathrm{196}−\mathrm{75}{x}^{\mathrm{2}} \\ $$$$\:\:\:\:{For}\:{y}\:{being}\:{rational}\:\bigtriangleup\:{must}\:{be} \\ $$$${perfect}\:{square}. \\ $$$$\mathrm{196}−\mathrm{75}{x}^{\mathrm{2}} \:{is}\:{perfect}\:{square}\:{for} \\ $$$${x}=\mathrm{0},\pm\mathrm{1}\:{only},{because}\:{x}\geqslant\mathrm{2}\:\bigtriangleup\:{is}\:−{ve} \\ $$$${and}\:{y}\:{will}\:{be}\:{imaginary}. \\ $$$${x}=\mathrm{0}\Rightarrow{y}=\frac{−\left(\mathrm{5}\left(\mathrm{0}\right)−\mathrm{14}\right)\pm\sqrt{\mathrm{196}−\mathrm{75}\left(\mathrm{0}\right)^{\mathrm{2}} }}{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{14}\pm\mathrm{14}}{\mathrm{10}}=\mathrm{0},\frac{\mathrm{14}}{\mathrm{5}} \\ $$$$\left(\mathrm{0},\mathrm{0}\right)\:{is}\:{not}\:{acceptable},{because}\:{it} \\ $$$${doesn}'{t}\:{satisfy}\:\:{the}\:{original}\:{equatkon}. \\ $$$$\left({x},{y}\right)=\left(\mathrm{0},\frac{\mathrm{14}}{\mathrm{5}}\right) \\ $$$${x}=\mathrm{1},{y}=\frac{−\left(\mathrm{5}−\mathrm{14}\right)\pm\mathrm{11}}{\mathrm{10}}=\frac{\mathrm{9}\pm\mathrm{11}}{\mathrm{10}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{y}=\mathrm{2},−\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\left({x},{y}\right)=\left(\mathrm{1},\mathrm{2}\right)\left(\mathrm{1},−\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$$${x}=−\mathrm{1}\Rightarrow{y}=\frac{−\left(\mathrm{5}\left(−\mathrm{1}\right)−\mathrm{14}\right)\pm\mathrm{11}}{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{5}+\mathrm{14}\pm\mathrm{11}}{\mathrm{10}}=\mathrm{3},\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\left({x},{y}\right)=\left(−\mathrm{1},\mathrm{3}\right),\left(−\mathrm{1},\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$
Commented by mathdanisur last updated on 01/Oct/21
$$\mathrm{Very}\:\mathrm{nice}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mathdanisur last updated on 30/Sep/21
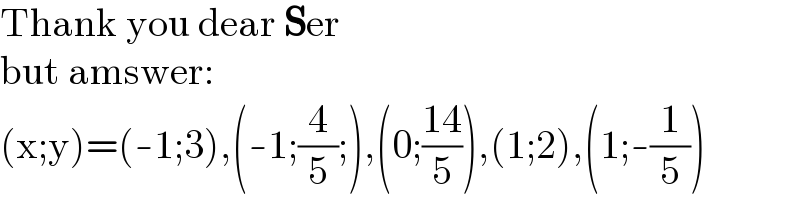
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$$$\mathrm{but}\:\mathrm{amswer}: \\ $$$$\left(\mathrm{x};\mathrm{y}\right)=\left(-\mathrm{1};\mathrm{3}\right),\left(-\mathrm{1};\frac{\mathrm{4}}{\mathrm{5}};\right),\left(\mathrm{0};\frac{\mathrm{14}}{\mathrm{5}}\right),\left(\mathrm{1};\mathrm{2}\right),\left(\mathrm{1};-\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 30/Sep/21
$$\mathrm{I}'{ve}\:{revised}\:{my}\:{answer}\:{and}\:{now}\:{it} \\ $$$${consist}\:{of}\:{all}\:{the}\:{answers}. \\ $$
