
Question Number 155310 by SANOGO last updated on 28/Sep/21
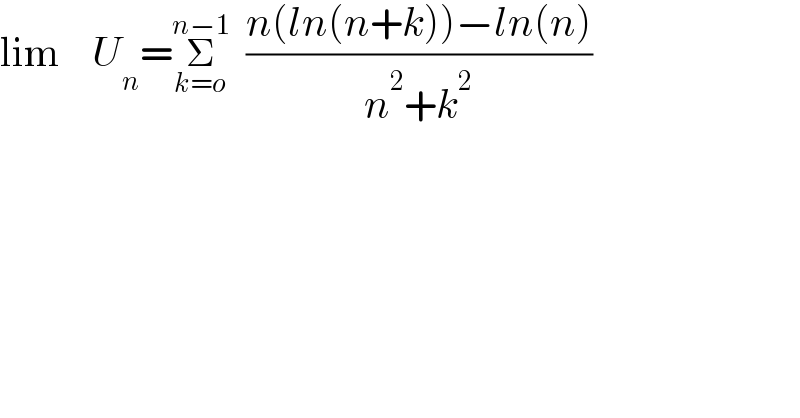
$$\mathrm{lim}\:\:\:\:{U}_{{n}} =\underset{{k}={o}} {\overset{{n}−\mathrm{1}} {\sum}}\:\:\frac{{n}\left({ln}\left({n}+{k}\right)\right)−{ln}\left({n}\right)}{{n}^{\mathrm{2}} +{k}^{\mathrm{2}} } \\ $$
Answered by puissant last updated on 28/Sep/21

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}{U}_{{n}} \:=\:\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{{n}\left({ln}\left(\frac{{n}+{k}}{{n}}\right)\right)}{{n}^{\mathrm{2}} +{k}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{U}_{{n}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{{ln}\left(\mathrm{1}+\left(\frac{{k}}{{n}}\right)\right)}{\mathrm{1}+\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} } \\ $$$${qui}\:{est}\:{sous}\:{la}\:{forme}\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{b}−{a}}{{n}}\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{f}\left({a}+{k}\frac{{b}−{a}}{{n}}\right) \\ $$$${qui}\:{est}\:{une}\:{Integrale}\:{de}\:{Riemann},{et}\:{donne}\:{alors}: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{U}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\:{Q} \\ $$$${x}={tant}\:\rightarrow\:{Q}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{ln}\left(\mathrm{1}+{tant}\right)}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)}\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tant}\right){dt}\:;\:{u}=\frac{\pi}{\mathrm{4}}−{t}\rightarrow{dt}=−{du} \\ $$$$\Rightarrow\:{Q}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{\mathrm{2}}{\mathrm{1}+{tanu}}\right){du}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\mathrm{2}{du}−{Q} \\ $$$$\Rightarrow\:\mathrm{2}{Q}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\mathrm{2}\:{du}\:\Rightarrow\:{Q}=\frac{\pi}{\mathrm{8}}{ln}\mathrm{2}... \\ $$$$ \\ $$$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{U}_{{n}} \:=\:\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{{n}\left({ln}\left({n}+{k}\right)−{ln}\left({n}\right)\right)}{{n}^{\mathrm{2}} +{k}^{\mathrm{2}} }\:=\:\frac{\pi}{\mathrm{8}}{ln}\mathrm{2}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\because\therefore......\mathscr{L}{e}\:{puissant}........ \\ $$
Commented by SANOGO last updated on 28/Sep/21

$${tu}\:{est}\:{vraiment}\:{puissant}\:{merci} \\ $$
Commented by Tawa11 last updated on 28/Sep/21

$$\mathrm{nice}\:\mathrm{sir} \\ $$
