
Question Number 155295 by mathdanisur last updated on 28/Sep/21
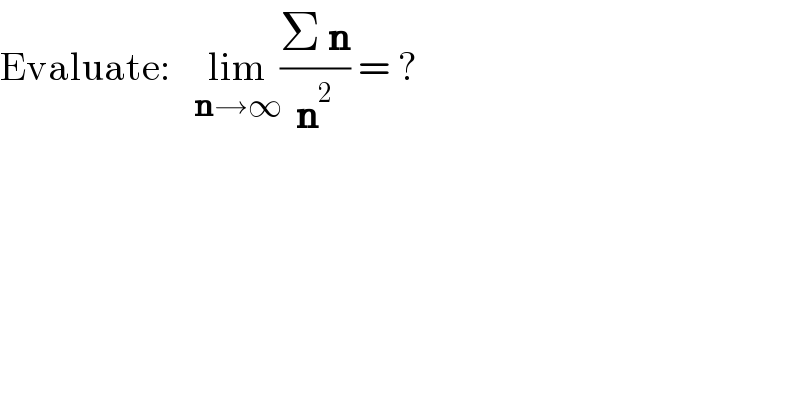
$$\mathrm{Evaluate}:\:\:\:\underset{\boldsymbol{\mathrm{n}}\rightarrow\infty} {\mathrm{lim}}\frac{\Sigma\:\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\:=\:? \\ $$
Commented by mathdanisur last updated on 28/Sep/21
$$\mathrm{Very}\:\mathrm{nice}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by MJS_new last updated on 28/Sep/21
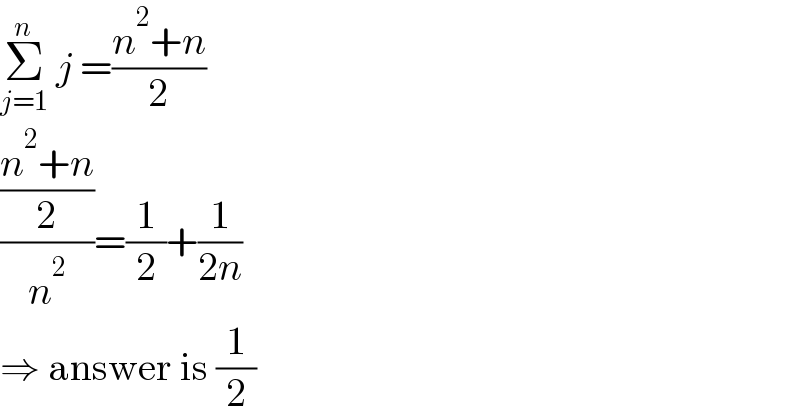
$$\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\:{j}\:=\frac{{n}^{\mathrm{2}} +{n}}{\mathrm{2}} \\ $$$$\frac{\frac{{n}^{\mathrm{2}} +{n}}{\mathrm{2}}}{{n}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
