
Question Number 155189 by qaz last updated on 27/Sep/21

$$\mathrm{How}\:\mathrm{to}\:\mathrm{extract}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\:\mathrm{term}\:``\mathrm{x}^{\mathrm{n}} \mathrm{y}^{\mathrm{m}} \:''\:\:\mathrm{in}\:\left(\mathrm{1}+\frac{\mathrm{yx}}{\mathrm{1}−\mathrm{x}}\right)\left(\mathrm{1}−\frac{\mathrm{yx}}{\mathrm{1}−\mathrm{x}}\right)^{−\mathrm{1}} ? \\ $$
Answered by mr W last updated on 26/Sep/21
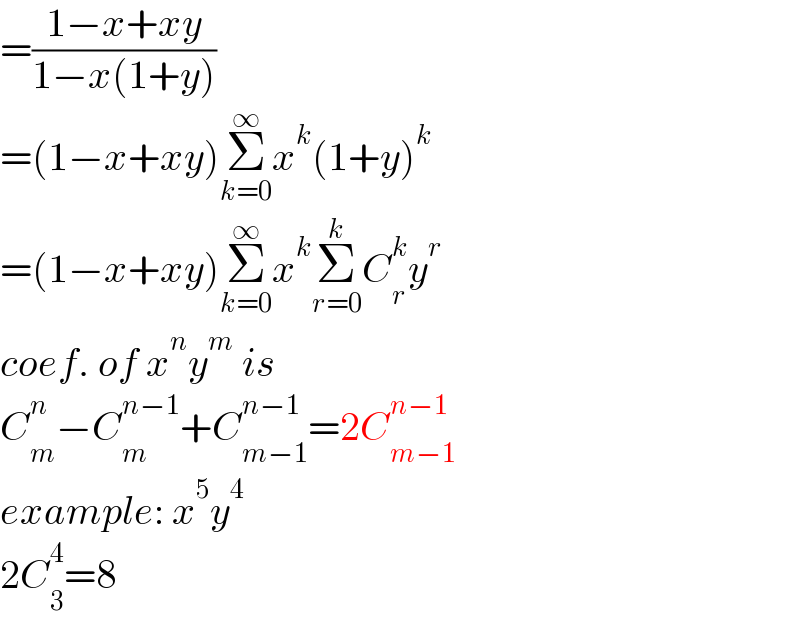
$$=\frac{\mathrm{1}−{x}+{xy}}{\mathrm{1}−{x}\left(\mathrm{1}+{y}\right)} \\ $$$$=\left(\mathrm{1}−{x}+{xy}\right)\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{k}} \left(\mathrm{1}+{y}\right)^{{k}} \\ $$$$=\left(\mathrm{1}−{x}+{xy}\right)\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{k}} \underset{{r}=\mathrm{0}} {\overset{{k}} {\sum}}{C}_{{r}} ^{{k}} {y}^{{r}} \\ $$$${coef}.\:{of}\:{x}^{{n}} {y}^{{m}} \:{is} \\ $$$${C}_{{m}} ^{{n}} −{C}_{{m}} ^{{n}−\mathrm{1}} +{C}_{{m}−\mathrm{1}} ^{{n}−\mathrm{1}} =\mathrm{2}{C}_{{m}−\mathrm{1}} ^{{n}−\mathrm{1}} \\ $$$${example}:\:{x}^{\mathrm{5}} {y}^{\mathrm{4}} \\ $$$$\mathrm{2}{C}_{\mathrm{3}} ^{\mathrm{4}} =\mathrm{8} \\ $$
Commented by Tawa11 last updated on 26/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
Commented by qaz last updated on 27/Sep/21

$$\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot}.\mathrm{mr}\:\mathrm{W} \\ $$
