
Question Number 155153 by mathdanisur last updated on 26/Sep/21
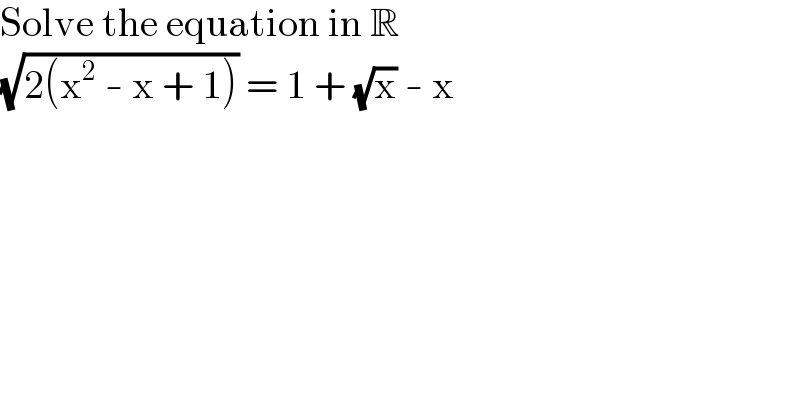
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{in}\:\mathbb{R} \\ $$$$\sqrt{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} \:-\:\mathrm{x}\:+\:\mathrm{1}\right)}\:=\:\mathrm{1}\:+\:\sqrt{\mathrm{x}}\:-\:\mathrm{x} \\ $$
Answered by MJS_new last updated on 26/Sep/21
![(√x)∈R ⇒ x≥0 but it′s easy to see x≠0 and lhs>0 ⇒ 1+(√x)−x>0 ⇒ 0<x<(3/2)+((√5)/2) let x=t^2 ∧t>0 (√(2(t^4 −t^2 +1)))=−t^2 +t+1 [⇒ 0<t<(1/2)+((√5)/2)] squaring 2(t^4 −t^2 +1)=(t^2 −t−1)^2 t^4 +2t^3 −t^2 −2t+1=0 (t^2 +t+1)^2 =0 ⇒ t=−(1/2)+((√5)/2) ⇒ x=(3/2)−((√5)/2)](Q155171.png)
$$\sqrt{{x}}\in\mathbb{R}\:\Rightarrow\:{x}\geqslant\mathrm{0}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:{x}\neq\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{lhs}>\mathrm{0}\:\Rightarrow\:\mathrm{1}+\sqrt{{x}}−{x}>\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{0}<{x}<\frac{\mathrm{3}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{let}\:{x}={t}^{\mathrm{2}} \wedge{t}>\mathrm{0} \\ $$$$\sqrt{\mathrm{2}\left({t}^{\mathrm{4}} −{t}^{\mathrm{2}} +\mathrm{1}\right)}=−{t}^{\mathrm{2}} +{t}+\mathrm{1}\:\left[\Rightarrow\:\mathrm{0}<{t}<\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right] \\ $$$$\mathrm{squaring} \\ $$$$\mathrm{2}\left({t}^{\mathrm{4}} −{t}^{\mathrm{2}} +\mathrm{1}\right)=\left({t}^{\mathrm{2}} −{t}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$${t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{3}} −{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:{t}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{3}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 26/Sep/21
$$\mathrm{awesome}\:\mathrm{solution},\:\mathrm{thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
