
Question Number 155144 by mnjuly1970 last updated on 26/Sep/21
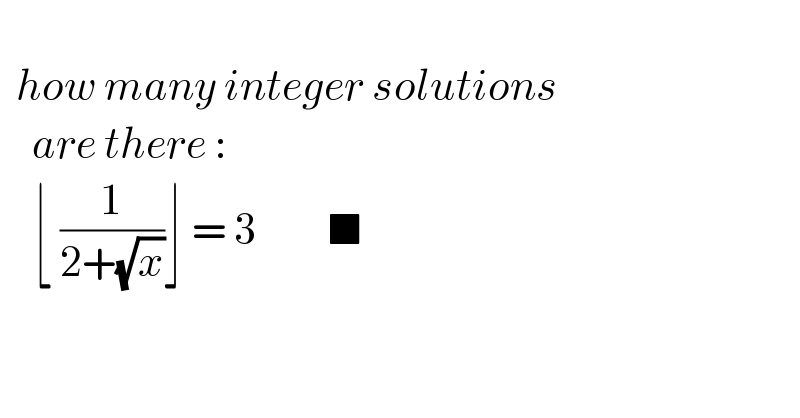
$$ \\ $$$$\:\:{how}\:{many}\:{integer}\:{solutions}\: \\ $$$$\:\:\:\:{are}\:{there}\:: \\ $$$$\:\:\:\:\lfloor\:\frac{\mathrm{1}}{\mathrm{2}+\sqrt{{x}}}\rfloor\:=\:\mathrm{3}\:\:\:\:\:\:\:\:\:\blacksquare \\ $$$$ \\ $$
Commented by mr W last updated on 26/Sep/21
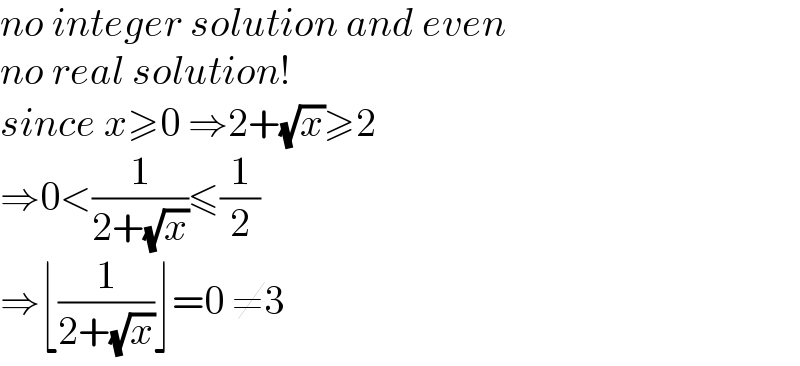
$${no}\:{integer}\:{solution}\:{and}\:{even} \\ $$$${no}\:{real}\:{solution}! \\ $$$${since}\:{x}\geqslant\mathrm{0}\:\Rightarrow\mathrm{2}+\sqrt{{x}}\geqslant\mathrm{2} \\ $$$$\Rightarrow\mathrm{0}<\frac{\mathrm{1}}{\mathrm{2}+\sqrt{{x}}}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\lfloor\frac{\mathrm{1}}{\mathrm{2}+\sqrt{{x}}}\rfloor=\mathrm{0}\:\neq\mathrm{3} \\ $$
Commented by mnjuly1970 last updated on 26/Sep/21
$${grateful}...{mr}\:{W} \\ $$
Commented by talminator2856791 last updated on 26/Sep/21
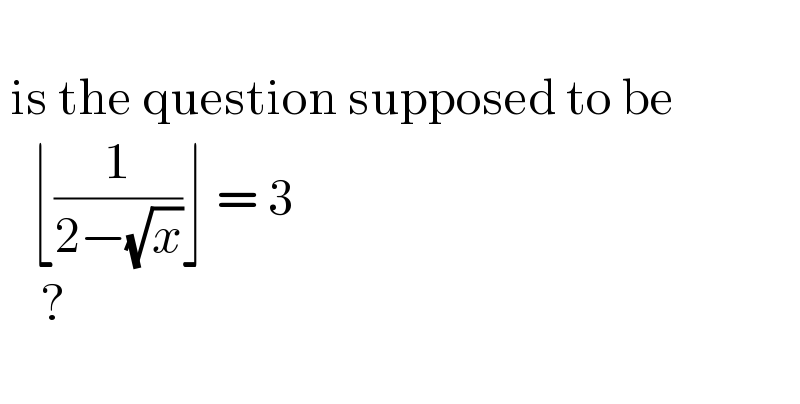
$$\: \\ $$$$\:\mathrm{is}\:\mathrm{the}\:\mathrm{question}\:\mathrm{supposed}\:\mathrm{to}\:\mathrm{be} \\ $$$$\:\:\:\lfloor\frac{\mathrm{1}}{\mathrm{2}−\sqrt{{x}}}\rfloor\:=\:\mathrm{3} \\ $$$$\:\:\:\:? \\ $$$$\: \\ $$
