
Question Number 83859 by john santu last updated on 06/Mar/20
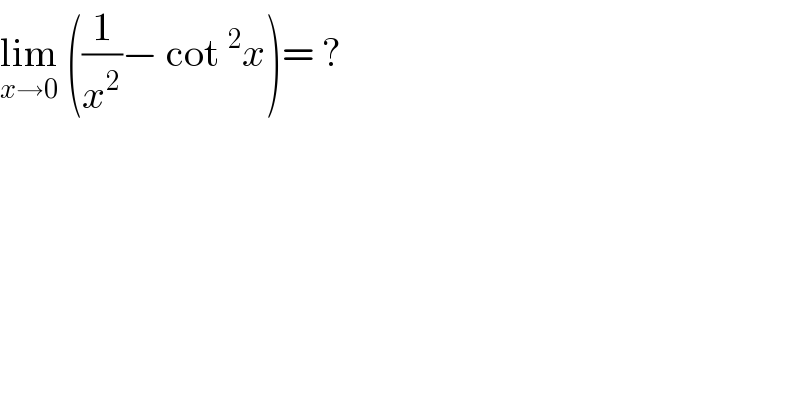
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\:\mathrm{cot}\:^{\mathrm{2}} {x}\right)=\:? \\ $$
Commented by john santu last updated on 06/Mar/20
![lim_(x→0) ((1/x^2 )−(1/(tan^2 x))) = lim_(x→0) ((((tan x−x)(tan x+x))/(x^2 tan^2 x))) = lim_(x→0) (((tan x+x)/x)) × lim_(x→0) (((tan x−x)/(x tan^2 x))) = 2 × lim_(x→0) (((1/2)sin 2x − xcos^2 x)/(x sin^2 x)) = 2 × lim_(x→0) ((cos 2x−[cos^2 x−xsin 2x])/(sin^2 x+x sin 2x)) 2 × lim_(x→0) ((cos^2 x−1+xsin 2x)/(sin^2 x+xsin 2x)) 2 ×lim_(x→0) ((−x^2 +2x^2 )/(3x^2 )) = (2/3)](Q83860.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{tan}\:^{\mathrm{2}} {x}}\right)\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\left(\mathrm{tan}\:{x}−{x}\right)\left(\mathrm{tan}\:{x}+{x}\right)}{{x}^{\mathrm{2}} \:\mathrm{tan}\:^{\mathrm{2}} {x}}\right)\:=\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{tan}\:{x}+{x}}{{x}}\right)\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{tan}\:{x}−{x}}{{x}\:\mathrm{tan}^{\mathrm{2}} \:{x}}\right)\:= \\ $$$$\mathrm{2}\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}{x}\:−\:{x}\mathrm{cos}^{\mathrm{2}} \:{x}}{{x}\:\mathrm{sin}^{\mathrm{2}} \:{x}}\:=\: \\ $$$$\mathrm{2}\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\mathrm{2}{x}−\left[\mathrm{cos}\:^{\mathrm{2}} {x}−{x}\mathrm{sin}\:\mathrm{2}{x}\right]}{\mathrm{sin}\:^{\mathrm{2}} {x}+{x}\:\mathrm{sin}\:\mathrm{2}{x}} \\ $$$$\mathrm{2}\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{1}+{x}\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{sin}\:^{\mathrm{2}} {x}+{x}\mathrm{sin}\:\mathrm{2}{x}} \\ $$$$\mathrm{2}\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−{x}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{3}{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$
