
Question Number 154892 by mathdanisur last updated on 22/Sep/21
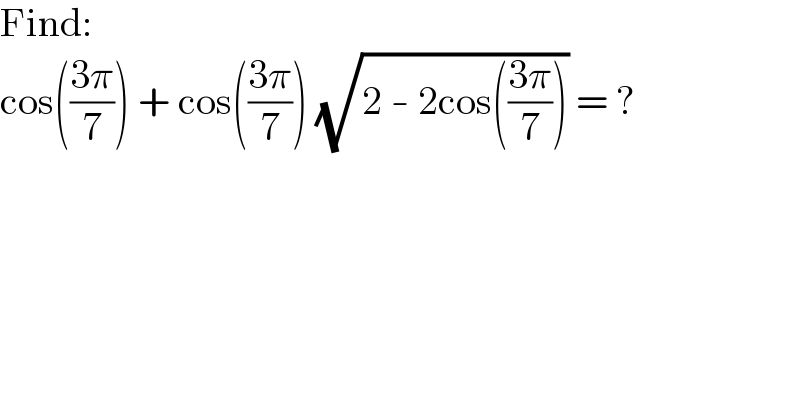
$$\mathrm{Find}: \\ $$$$\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right)\:+\:\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right)\:\sqrt{\mathrm{2}\:-\:\mathrm{2cos}\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right)}\:=\:? \\ $$
Commented by MJS_new last updated on 23/Sep/21

$$\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 23/Sep/21
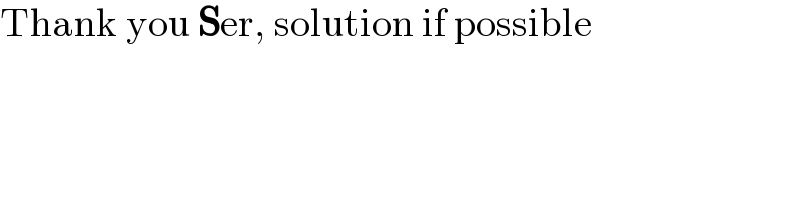
$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{solution}\:\mathrm{if}\:\mathrm{possible} \\ $$
Answered by mnjuly1970 last updated on 23/Sep/21
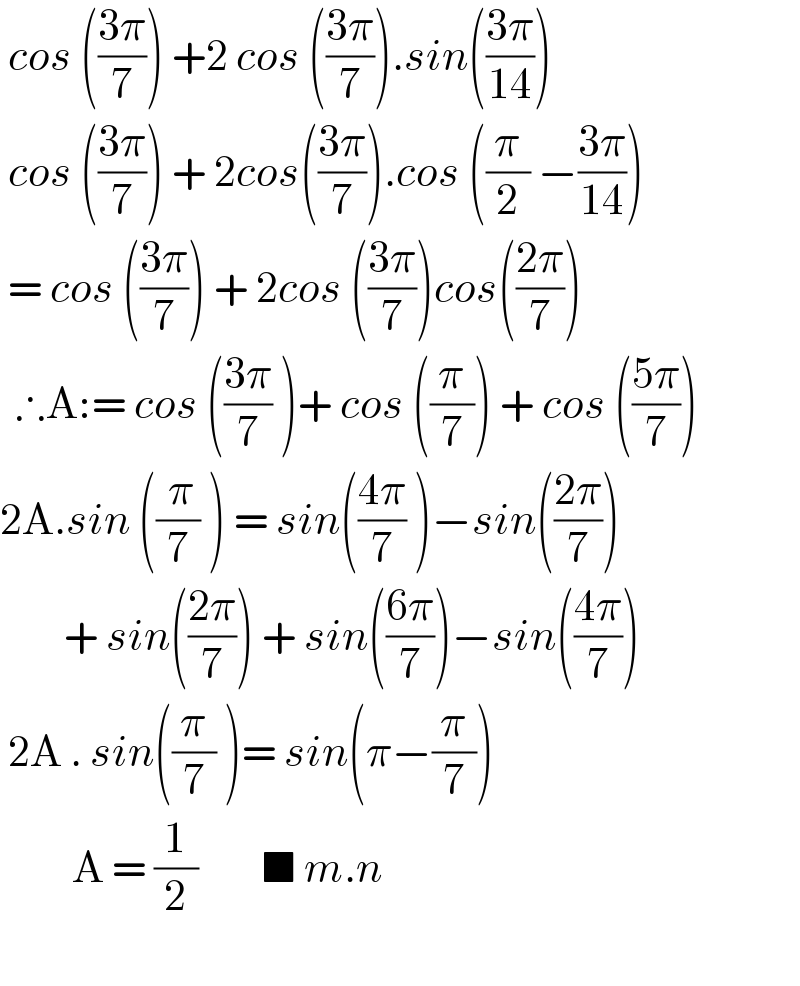
$$\:{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right)\:+\mathrm{2}\:{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right).{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{14}}\right) \\ $$$$\:{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right)\:+\:\mathrm{2}{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right).{cos}\:\left(\frac{\pi}{\mathrm{2}}\:−\frac{\mathrm{3}\pi}{\mathrm{14}}\right)\: \\ $$$$\:=\:{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right)\:+\:\mathrm{2}{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\right){cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right) \\ $$$$\:\:\therefore\mathrm{A}:=\:{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{7}}\:\right)+\:{cos}\:\left(\frac{\pi}{\mathrm{7}}\right)\:+\:{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{7}}\right) \\ $$$$\mathrm{2A}.{sin}\:\left(\frac{\:\pi}{\mathrm{7}}\:\right)\:=\:{sin}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\:\right)−{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right) \\ $$$$\:\:\:\:\:\:\:\:+\:{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\:+\:{sin}\left(\frac{\mathrm{6}\pi}{\mathrm{7}}\right)−{sin}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right) \\ $$$$\:\mathrm{2A}\:.\:{sin}\left(\frac{\pi}{\mathrm{7}}\:\right)=\:{sin}\left(\pi−\frac{\pi}{\mathrm{7}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{A}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\blacksquare\:{m}.{n} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 23/Sep/21
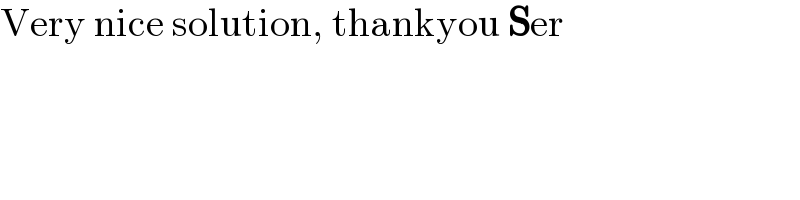
$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{solution},\:\mathrm{thankyou}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
Commented by mnjuly1970 last updated on 23/Sep/21

$$\:{thsnkz}\:{alot}\:{sir} \\ $$
