
Question Number 154649 by mathdanisur last updated on 20/Sep/21
![if n ∈ N^(>2) prove that [((n)^(1/3) + ((n + 2))^(1/3) )^3 ] + 1 = 0 (mod 8)](Q154649.png)
$$\mathrm{if}\:\:\mathrm{n}\:\in\:\mathbb{N}^{>\mathrm{2}} \:\:\mathrm{prove}\:\mathrm{that} \\ $$ $$\left[\left(\sqrt[{\mathrm{3}}]{\mathrm{n}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{n}\:+\:\mathrm{2}}\:\right)^{\mathrm{3}} \right]\:+\:\mathrm{1}\:=\:\mathrm{0}\:\left(\mathrm{mod}\:\mathrm{8}\right) \\ $$
Commented byMJS_new last updated on 20/Sep/21
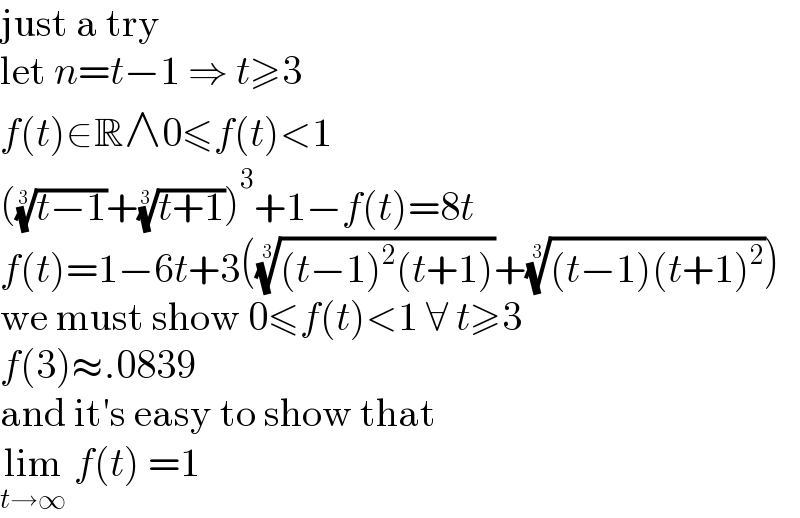
$$\mathrm{just}\:\mathrm{a}\:\mathrm{try} \\ $$ $$\mathrm{let}\:{n}={t}−\mathrm{1}\:\Rightarrow\:{t}\geqslant\mathrm{3} \\ $$ $${f}\left({t}\right)\in\mathbb{R}\wedge\mathrm{0}\leqslant{f}\left({t}\right)<\mathrm{1} \\ $$ $$\left(\sqrt[{\mathrm{3}}]{{t}−\mathrm{1}}+\sqrt[{\mathrm{3}}]{{t}+\mathrm{1}}\right)^{\mathrm{3}} +\mathrm{1}−{f}\left({t}\right)=\mathrm{8}{t} \\ $$ $${f}\left({t}\right)=\mathrm{1}−\mathrm{6}{t}+\mathrm{3}\left(\sqrt[{\mathrm{3}}]{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \left({t}+\mathrm{1}\right)}+\sqrt[{\mathrm{3}}]{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$ $$\mathrm{we}\:\mathrm{must}\:\mathrm{show}\:\mathrm{0}\leqslant{f}\left({t}\right)<\mathrm{1}\:\forall\:{t}\geqslant\mathrm{3} \\ $$ $${f}\left(\mathrm{3}\right)\approx.\mathrm{0839} \\ $$ $$\mathrm{and}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{show}\:\mathrm{that} \\ $$ $$\underset{{t}\rightarrow\infty} {\mathrm{lim}}\:{f}\left({t}\right)\:=\mathrm{1} \\ $$
Commented bymathdanisur last updated on 20/Sep/21
$$\mathrm{Very}\:\mathrm{nice}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you} \\ $$
