
Question Number 154547 by peter frank last updated on 19/Sep/21

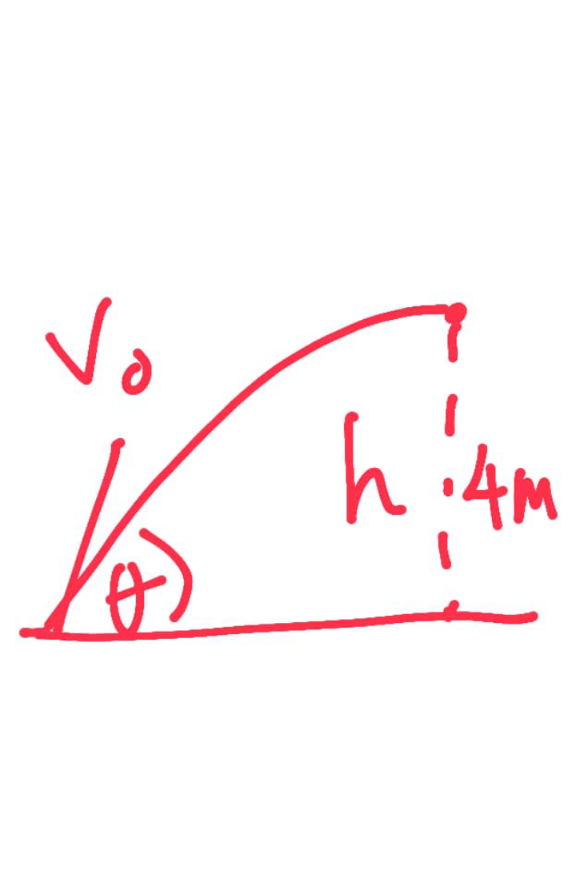
$$\mathrm{A}\:\mathrm{particle}\:\mathrm{is}\:\mathrm{projected}\:\mathrm{inside}\:\mathrm{the}\:\mathrm{tunnel} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{4m}\:\mathrm{high}.\mathrm{if}\:\:\mathrm{the}\:\mathrm{initial}\:\mathrm{speed} \\ $$$$\mathrm{is}\:\mathrm{V}_{\mathrm{o}} .\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{maximum} \\ $$$$\mathrm{range}\:\mathrm{inside}\:\mathrm{the}\:\mathrm{tunnel}\:\mathrm{is}\:\mathrm{given} \\ $$$$\mathrm{by}\:\:\:\:\:\:\mathrm{R}=\mathrm{4}\sqrt{\mathrm{2}}\:\sqrt{\frac{\mathrm{V}_{\mathrm{o}} ^{\mathrm{2}} }{\mathrm{g}}−\mathrm{8}} \\ $$
Answered by peter frank last updated on 20/Sep/21
Commented by peter frank last updated on 20/Sep/21

$$\mathrm{Range}=\frac{\mathrm{2v}_{\mathrm{o}} ^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{g}} \\ $$$$\mathrm{H}_{\mathrm{max}} =\frac{\mathrm{v}_{\mathrm{o}} ^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{g}}=\mathrm{4m} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \theta=\frac{\mathrm{8g}}{\mathrm{v}_{\mathrm{o}} ^{\mathrm{2}} }\:\:\:\: \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{2}\sqrt{\mathrm{2g}}}{\mathrm{v}_{\mathrm{o}} } \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \theta=\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \theta} \\ $$$$\mathrm{cos}\:\theta=\frac{\mathrm{1}}{\mathrm{v}_{\mathrm{o}} }\sqrt{\mathrm{v}_{\mathrm{o}} ^{\mathrm{2}} −\mathrm{8g}} \\ $$$$\mathrm{Range}=\frac{\mathrm{2v}_{\mathrm{o}} ^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{g}} \\ $$$$\mathrm{Range}=\frac{\mathrm{2v}_{\mathrm{o}} ^{\mathrm{2}} \:\frac{\mathrm{2}\sqrt{\mathrm{2g}}}{\mathrm{v}_{\mathrm{o}} }\:\frac{\mathrm{1}}{\mathrm{v}_{\mathrm{o}} }\sqrt{\mathrm{v}_{\mathrm{o}} ^{\mathrm{2}} −\mathrm{8g}}\:\:}{\mathrm{g}} \\ $$$$\mathrm{R}=\frac{\mathrm{4}\sqrt{\mathrm{2g}}}{\mathrm{g}}\sqrt{\mathrm{v}_{\mathrm{o}} ^{\mathrm{2}} −\mathrm{8g}} \\ $$$$\mathrm{R}=\mathrm{4}\sqrt{\mathrm{2}}\:\frac{\sqrt{\mathrm{g}}}{\mathrm{g}}\sqrt{\mathrm{v}_{\mathrm{o}} ^{\mathrm{2}} −\mathrm{8g}} \\ $$$$\mathrm{but}\:\:\frac{\sqrt{\mathrm{g}}}{\mathrm{g}}=\sqrt{\frac{\mathrm{g}}{\mathrm{g}^{\mathrm{2}} }} \\ $$$$\mathrm{R}=\mathrm{4}\sqrt{\mathrm{2}\:}\:.\sqrt{\frac{\mathrm{g}}{\mathrm{g}^{\mathrm{2}} }\:\:\:\mathrm{v}_{\mathrm{o}} ^{\mathrm{2}} −\mathrm{8g}} \\ $$$$\mathrm{R}=\mathrm{4}\sqrt{\mathrm{2}\:}\:.\sqrt{\frac{\mathrm{1}}{\mathrm{g}}\:.\:\mathrm{v}_{\mathrm{o}} ^{\mathrm{2}} −\mathrm{8g}} \\ $$$$\mathrm{R}=\mathrm{4}\sqrt{\mathrm{2}\:}\:.\sqrt{\frac{\mathrm{v}_{\mathrm{o}} ^{\mathrm{2}} }{\mathrm{g}}−\mathrm{8}} \\ $$$$ \\ $$
Commented by mr W last updated on 20/Sep/21

$${well}\:{solved}! \\ $$
Commented by peter frank last updated on 21/Sep/21

$$\mathrm{thank}\:\mathrm{you}. \\ $$
Commented by Tawa11 last updated on 21/Sep/21

$$\mathrm{nice}\:\mathrm{sir} \\ $$
