
Question Number 154409 by mnjuly1970 last updated on 18/Sep/21
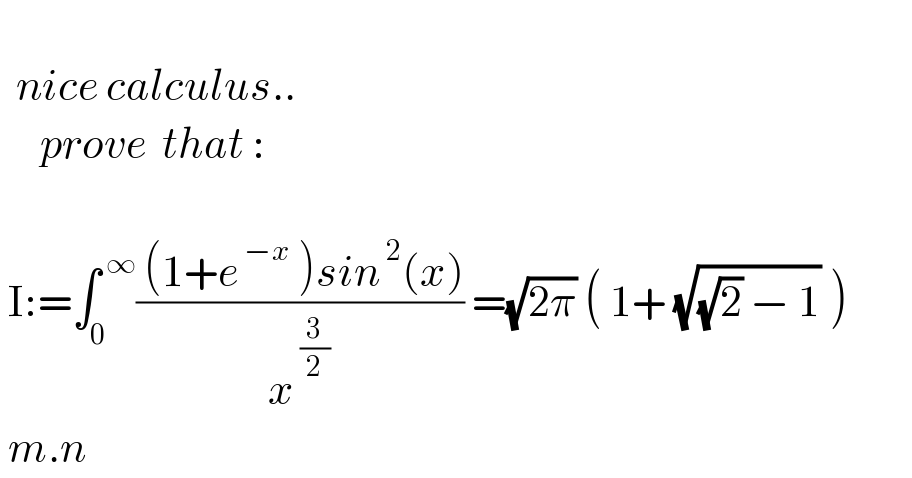
$$ \\ $$$$\:\:{nice}\:{calculus}.. \\ $$$$\:\:\:\:\:{prove}\:\:{that}\:: \\ $$$$\: \\ $$$$\:\mathrm{I}:=\int_{\mathrm{0}} ^{\:\infty} \frac{\:\left(\mathrm{1}+{e}^{\:−{x}} \:\right){sin}^{\:\mathrm{2}} \left({x}\right)}{{x}^{\:\frac{\mathrm{3}}{\mathrm{2}}} }\:=\sqrt{\mathrm{2}\pi}\:\left(\:\mathrm{1}+\:\sqrt{\sqrt{\mathrm{2}}\:−\:\mathrm{1}}\:\right) \\ $$$$\:{m}.{n} \\ $$
Answered by Kamel last updated on 18/Sep/21
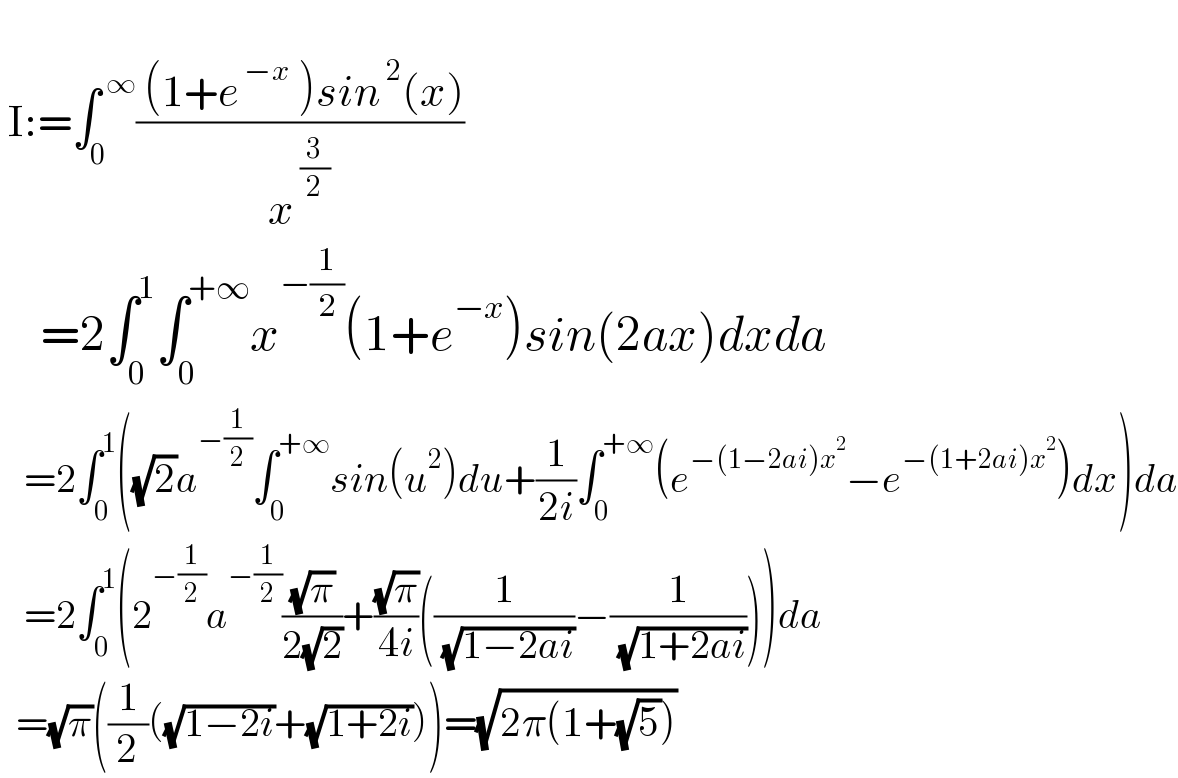
$$ \\ $$$$\:\mathrm{I}:=\int_{\mathrm{0}} ^{\:\infty} \frac{\:\left(\mathrm{1}+{e}^{\:−{x}} \:\right){sin}^{\:\mathrm{2}} \left({x}\right)}{{x}^{\:\frac{\mathrm{3}}{\mathrm{2}}} }\: \\ $$$$\:\:\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{+\infty} {x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}+{e}^{−{x}} \right){sin}\left(\mathrm{2}{ax}\right){dxda} \\ $$$$\:\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sqrt{\mathrm{2}}{a}^{−\frac{\mathrm{1}}{\mathrm{2}}} \int_{\mathrm{0}} ^{+\infty} {sin}\left({u}^{\mathrm{2}} \right){du}+\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{+\infty} \left({e}^{−\left(\mathrm{1}−\mathrm{2}{ai}\right){x}^{\mathrm{2}} } −{e}^{−\left(\mathrm{1}+\mathrm{2}{ai}\right){x}^{\mathrm{2}} } \right){dx}\right){da} \\ $$$$\:\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}} {a}^{−\frac{\mathrm{1}}{\mathrm{2}}} \frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}+\frac{\sqrt{\pi}}{\mathrm{4}{i}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{2}{ai}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{2}{ai}}}\right)\right){da} \\ $$$$\:\:=\sqrt{\pi}\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{1}−\mathrm{2}{i}}+\sqrt{\mathrm{1}+\mathrm{2}{i}}\right)\right)=\sqrt{\mathrm{2}\pi\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)} \\ $$
