
Question Number 154401 by mathdanisur last updated on 18/Sep/21
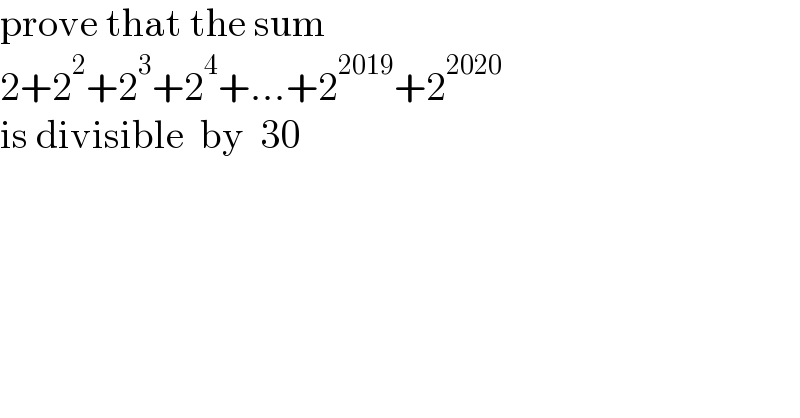
$$\mathrm{prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{sum} \\ $$$$\mathrm{2}+\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{4}} +...+\mathrm{2}^{\mathrm{2019}} +\mathrm{2}^{\mathrm{2020}} \\ $$$$\mathrm{is}\:\mathrm{divisible}\:\:\mathrm{by}\:\:\mathrm{30} \\ $$
Answered by talminator2856791 last updated on 18/Sep/21
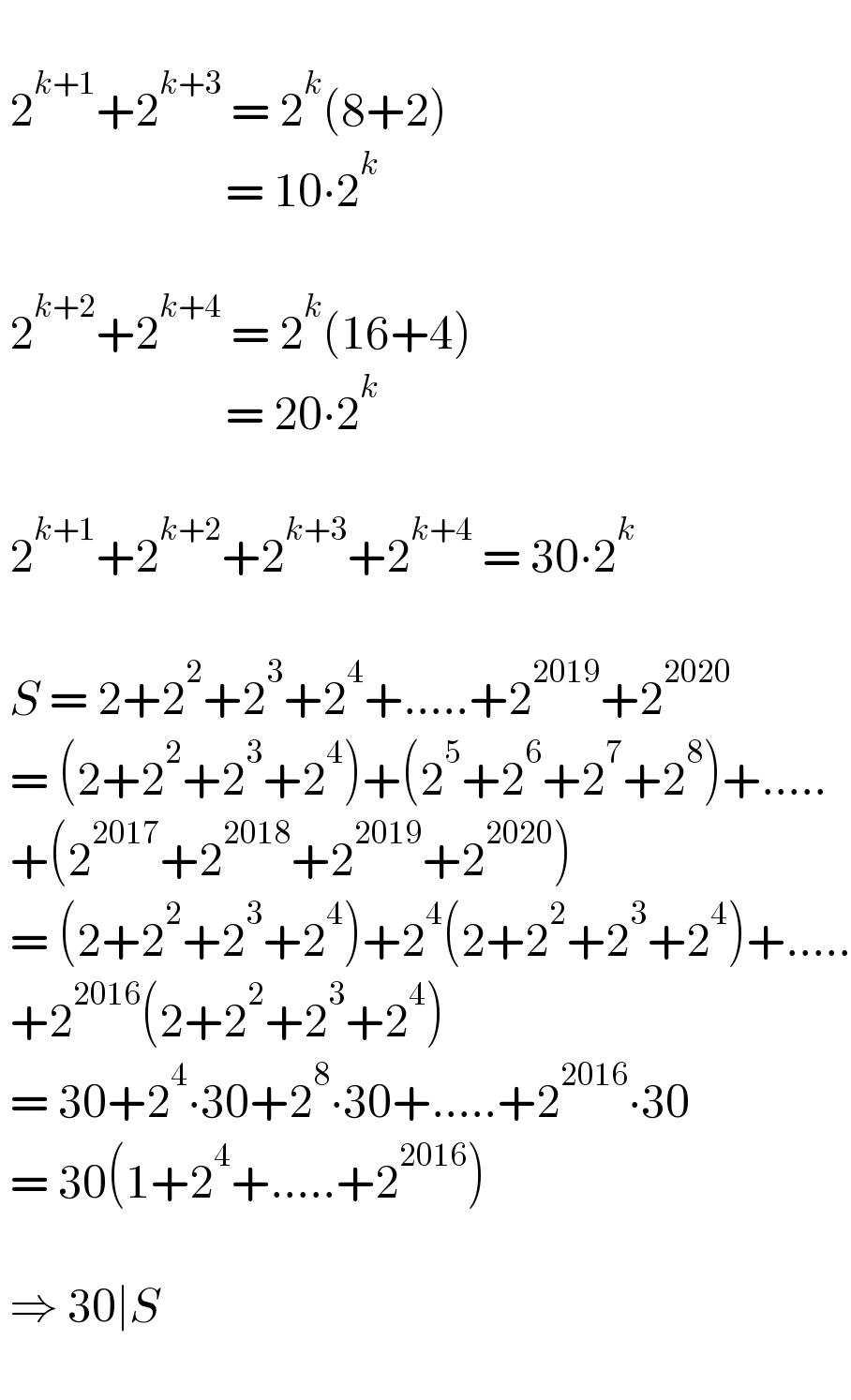
$$\: \\ $$$$\:\mathrm{2}^{{k}+\mathrm{1}} +\mathrm{2}^{{k}+\mathrm{3}} \:=\:\mathrm{2}^{{k}} \left(\mathrm{8}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{10}\centerdot\mathrm{2}^{{k}} \\ $$$$\: \\ $$$$\:\mathrm{2}^{{k}+\mathrm{2}} +\mathrm{2}^{{k}+\mathrm{4}} \:=\:\mathrm{2}^{{k}} \left(\mathrm{16}+\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{20}\centerdot\mathrm{2}^{{k}} \\ $$$$\: \\ $$$$\:\mathrm{2}^{{k}+\mathrm{1}} +\mathrm{2}^{{k}+\mathrm{2}} +\mathrm{2}^{{k}+\mathrm{3}} +\mathrm{2}^{{k}+\mathrm{4}} \:=\:\mathrm{30}\centerdot\mathrm{2}^{{k}} \\ $$$$\: \\ $$$$\:{S}\:=\:\mathrm{2}+\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{4}} +.....+\mathrm{2}^{\mathrm{2019}} +\mathrm{2}^{\mathrm{2020}} \\ $$$$\:=\:\left(\mathrm{2}+\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{4}} \right)+\left(\mathrm{2}^{\mathrm{5}} +\mathrm{2}^{\mathrm{6}} +\mathrm{2}^{\mathrm{7}} +\mathrm{2}^{\mathrm{8}} \right)+..... \\ $$$$\:+\left(\mathrm{2}^{\mathrm{2017}} +\mathrm{2}^{\mathrm{2018}} +\mathrm{2}^{\mathrm{2019}} +\mathrm{2}^{\mathrm{2020}} \right) \\ $$$$\:=\:\left(\mathrm{2}+\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{4}} \right)+\mathrm{2}^{\mathrm{4}} \left(\mathrm{2}+\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{4}} \right)+..... \\ $$$$\:+\mathrm{2}^{\mathrm{2016}} \left(\mathrm{2}+\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{4}} \right) \\ $$$$\:=\:\mathrm{30}+\mathrm{2}^{\mathrm{4}} \centerdot\mathrm{30}+\mathrm{2}^{\mathrm{8}} \centerdot\mathrm{30}+.....+\mathrm{2}^{\mathrm{2016}} \centerdot\mathrm{30} \\ $$$$\:=\:\mathrm{30}\left(\mathrm{1}+\mathrm{2}^{\mathrm{4}} +.....+\mathrm{2}^{\mathrm{2016}} \right) \\ $$$$\: \\ $$$$\:\Rightarrow\:\mathrm{30}\mid{S} \\ $$$$\: \\ $$
Commented by mathdanisur last updated on 18/Sep/21
$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{Ser}\:\mathrm{thanks} \\ $$
Answered by Rasheed.Sindhi last updated on 18/Sep/21

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underline{\mathbb{MOD}\:\mathrm{30}} \\ $$$$\mathrm{2}^{\mathrm{4}} \equiv\mathrm{16}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{2}^{\mathrm{4}×\mathrm{1}} \equiv\mathrm{16} \\ $$$$\left(\mathrm{2}^{\mathrm{4}} \right)^{\mathrm{2}} \equiv\left(\mathrm{16}\right)^{\mathrm{2}} \Rightarrow\mathrm{2}^{\mathrm{8}} \equiv\mathrm{16}\:\:\Rightarrow\mathrm{2}^{\mathrm{4}×\mathrm{2}} \equiv\mathrm{16} \\ $$$$\left(\mathrm{2}^{\mathrm{8}} \right)^{\mathrm{2}} \equiv\left(\mathrm{16}\right)^{\mathrm{2}} \Rightarrow\mathrm{2}^{\mathrm{12}} \equiv\mathrm{16}\Rightarrow\mathrm{2}^{\mathrm{4}×\mathrm{3}} \equiv\mathrm{16} \\ $$$$\ldots\:\:\:\ldots\:\:\:\ldots\:\:\:\ldots\:\:\:\ldots \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}^{\mathrm{4}×\mathrm{k}} \equiv\mathrm{16} \\ $$$$\mathrm{2}^{\mathrm{4k}} .\mathrm{2}\equiv\mathrm{16}.\mathrm{2}\equiv\mathrm{2}\Rightarrow\mathrm{2}^{\mathrm{4k}+\mathrm{1}} \equiv\mathrm{2} \\ $$$$\mathrm{2}^{\mathrm{4k}+\mathrm{1}} .\mathrm{2}\equiv\mathrm{2}.\mathrm{2}\equiv\mathrm{4}\Rightarrow\:\:\mathrm{2}^{\mathrm{4k}+\mathrm{2}} \equiv\mathrm{4} \\ $$$$\mathrm{2}^{\mathrm{4k}+\mathrm{2}} .\mathrm{2}\equiv\mathrm{4}.\mathrm{2}\equiv\mathrm{8}\Rightarrow\:\:\mathrm{2}^{\mathrm{4k}+\mathrm{3}} \equiv\mathrm{8} \\ $$$$\mathrm{2}^{\mathrm{4k}} \equiv\mathrm{16}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\mathrm{2}^{\mathrm{4k}} \:\equiv\:\mathrm{16} \\ $$$$\blacktriangleright\mathbb{S}=\mathrm{2}+\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{4}} +...+\mathrm{2}^{\mathrm{2019}} +\mathrm{2}^{\mathrm{2020}} \\ $$$$=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{505}} {\Sigma}}\left(\mathrm{2}^{\mathrm{4k}+\mathrm{1}} +\mathrm{2}^{\mathrm{4k}+\mathrm{2}} +\mathrm{2}^{\mathrm{4k}+\mathrm{3}} +\mathrm{2}^{\mathrm{4k}} \right) \\ $$$$\equiv\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{505}} {\Sigma}}\left(\mathrm{2}+\mathrm{4}+\mathrm{8}+\mathrm{16}\right).\mathrm{k}=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{505}} {\Sigma}}\left(\mathrm{30k}\right) \\ $$$$\mathbb{S}=\mathrm{30}×\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{505}} {\Sigma}}\mathrm{k} \\ $$$$\therefore\:\mathrm{30}\mid\mathbb{S} \\ $$
Commented by mathdanisur last updated on 18/Sep/21
$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{Ser}\:\mathrm{thankyou} \\ $$
Answered by JDamian last updated on 18/Sep/21
![S=2((2^(2020) −1)/(2−1))=2(2^(2020) −1) S=2^(2021) −2 S mod 30 =(2^(2021) −2) mod 30= =2^(2021) mod 30 −2 ∣(2^5 )^k mod 30 =(30+2)^k mod 30= =2^k mod 30 ∣ 2^(2021) mod 30 =[2∙(2^5 )^(404) ]mod 30= =(2∙2^(404) )mod 30=2^(405) mod 30= =(2^5 )^(81) mod 30=2^(81) mod 30= =2∙(2^5 )^(16) mod 30 =2^(17) mod 30= =2^2 (2^5 )^3 mod 30 = 2^5 mod 30 = 2 S mod 30 = 2 − 2 = 0](Q154496.png)
$${S}=\mathrm{2}\frac{\mathrm{2}^{\mathrm{2020}} −\mathrm{1}}{\mathrm{2}−\mathrm{1}}=\mathrm{2}\left(\mathrm{2}^{\mathrm{2020}} −\mathrm{1}\right) \\ $$$${S}=\mathrm{2}^{\mathrm{2021}} −\mathrm{2} \\ $$$${S}\:{mod}\:\mathrm{30}\:=\left(\mathrm{2}^{\mathrm{2021}} −\mathrm{2}\right)\:{mod}\:\mathrm{30}= \\ $$$$=\mathrm{2}^{\mathrm{2021}} {mod}\:\mathrm{30}\:−\mathrm{2} \\ $$$$ \\ $$$$\mid\left(\mathrm{2}^{\mathrm{5}} \right)^{{k}} {mod}\:\mathrm{30}\:=\left(\mathrm{30}+\mathrm{2}\right)^{{k}} \:{mod}\:\mathrm{30}= \\ $$$$=\mathrm{2}^{{k}} \:{mod}\:\mathrm{30}\:\:\mid \\ $$$$ \\ $$$$\mathrm{2}^{\mathrm{2021}} {mod}\:\mathrm{30}\:=\left[\mathrm{2}\centerdot\left(\mathrm{2}^{\mathrm{5}} \right)^{\mathrm{404}} \right]{mod}\:\mathrm{30}= \\ $$$$=\left(\mathrm{2}\centerdot\mathrm{2}^{\mathrm{404}} \right){mod}\:\mathrm{30}=\mathrm{2}^{\mathrm{405}} {mod}\:\mathrm{30}= \\ $$$$=\left(\mathrm{2}^{\mathrm{5}} \right)^{\mathrm{81}} {mod}\:\mathrm{30}=\mathrm{2}^{\mathrm{81}} {mod}\:\mathrm{30}= \\ $$$$=\mathrm{2}\centerdot\left(\mathrm{2}^{\mathrm{5}} \right)^{\mathrm{16}} {mod}\:\mathrm{30}\:=\mathrm{2}^{\mathrm{17}} \:{mod}\:\mathrm{30}= \\ $$$$=\mathrm{2}^{\mathrm{2}} \left(\mathrm{2}^{\mathrm{5}} \right)^{\mathrm{3}} {mod}\:\mathrm{30}\:=\:\mathrm{2}^{\mathrm{5}} \:{mod}\:\mathrm{30}\:=\:\mathrm{2} \\ $$$$ \\ $$$${S}\:{mod}\:\mathrm{30}\:=\:\mathrm{2}\:−\:\mathrm{2}\:=\:\mathrm{0} \\ $$
Commented by mathdanisur last updated on 18/Sep/21
$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{Ser}\:\mathrm{thankyou} \\ $$
