
Question Number 154384 by mathdanisur last updated on 17/Sep/21
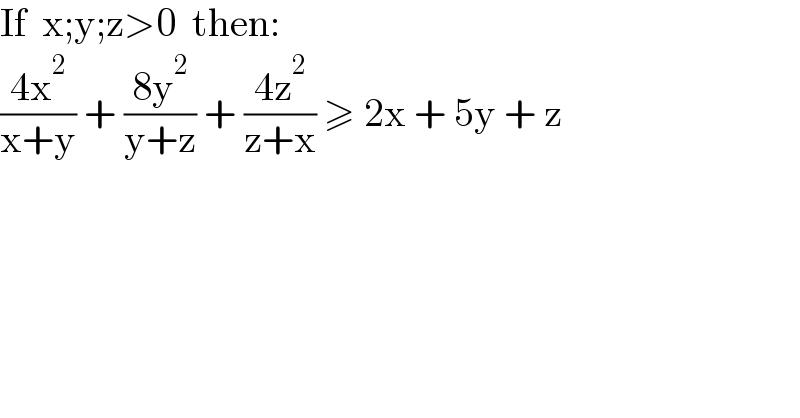
$$\mathrm{If}\:\:\mathrm{x};\mathrm{y};\mathrm{z}>\mathrm{0}\:\:\mathrm{then}: \\ $$ $$\frac{\mathrm{4x}^{\mathrm{2}} }{\mathrm{x}+\mathrm{y}}\:+\:\frac{\mathrm{8y}^{\mathrm{2}} }{\mathrm{y}+\mathrm{z}}\:+\:\frac{\mathrm{4z}^{\mathrm{2}} }{\mathrm{z}+\mathrm{x}}\:\geqslant\:\mathrm{2x}\:+\:\mathrm{5y}\:+\:\mathrm{z} \\ $$
Answered by ghimisi last updated on 18/Sep/21
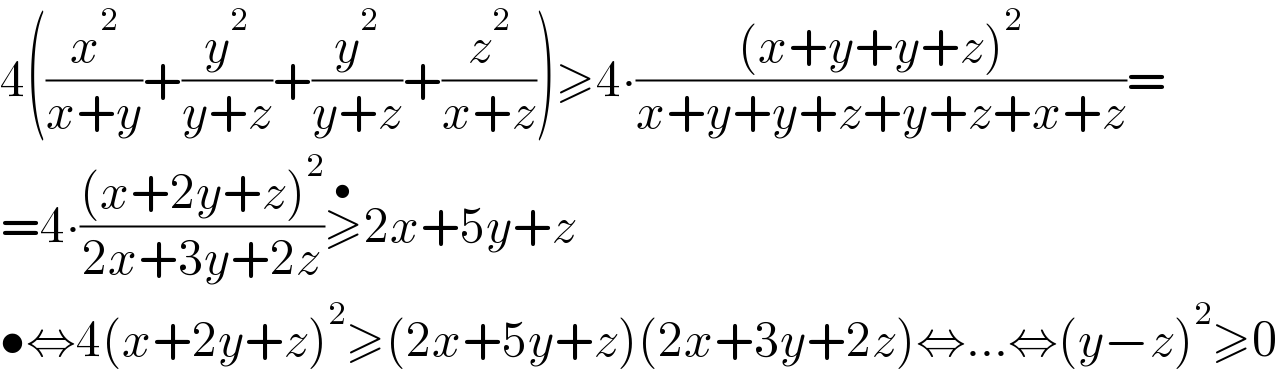
$$\mathrm{4}\left(\frac{{x}^{\mathrm{2}} }{{x}+{y}}+\frac{{y}^{\mathrm{2}} }{{y}+{z}}+\frac{{y}^{\mathrm{2}} }{{y}+{z}}+\frac{{z}^{\mathrm{2}} }{{x}+{z}}\right)\geqslant\mathrm{4}\centerdot\frac{\left({x}+{y}+{y}+{z}\right)^{\mathrm{2}} }{{x}+{y}+{y}+{z}+{y}+{z}+{x}+{z}}= \\ $$ $$=\mathrm{4}\centerdot\frac{\left({x}+\mathrm{2}{y}+{z}\right)^{\mathrm{2}} }{\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{2}{z}}\overset{\bullet} {\geqslant}\mathrm{2}{x}+\mathrm{5}{y}+{z} \\ $$ $$\bullet\Leftrightarrow\mathrm{4}\left({x}+\mathrm{2}{y}+{z}\right)^{\mathrm{2}} \geqslant\left(\mathrm{2}{x}+\mathrm{5}{y}+{z}\right)\left(\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{2}{z}\right)\Leftrightarrow...\Leftrightarrow\left({y}−{z}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$
Commented bymathdanisur last updated on 18/Sep/21
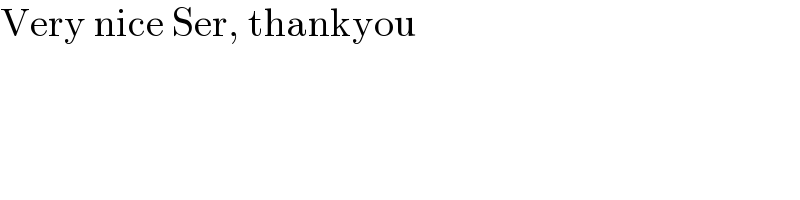
$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{Ser},\:\mathrm{thankyou} \\ $$
