
Question Number 154351 by ZiYangLee last updated on 17/Sep/21
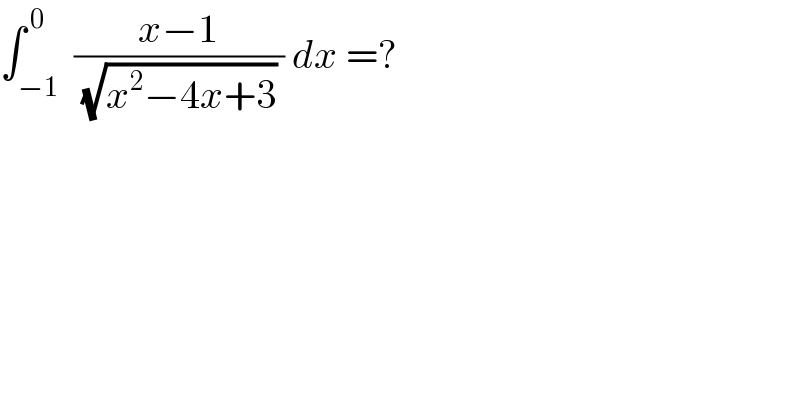
$$\int_{−\mathrm{1}} ^{\:\mathrm{0}} \:\frac{{x}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}\:}\:{dx}\:=? \\ $$
Answered by ZiYangLee last updated on 17/Sep/21
![∫_(−1) ^( 0) ((x−1)/( (√(x^2 −4x+3)) )) dx = ∫_(−1) ^( 0) (((x−2)+1)/( (√(x^2 −4x+3)) )) dx = ∫_(−1) ^( 0) (((1/2)(2x−4)+1)/( (√(x^2 −4x+3)) )) dx = ∫_(−1) ^( 0) (((2x−4)+2)/(2(√(x^2 −4x+3)) )) dx = ∫_(−1) ^( 0) ((2x−4)/(2(√(x^2 −4x+3)) )) dx +∫_(−1) ^( 0) (1/( (√(x^2 −4x+3)) )) dx let u=x^2 −4x+3 du=(2x−4) dx = ∫_8 ^( 3) (1/(2(√u) )) du +∫_(−1) ^( 0) (x^2 −4x+3)^(−(1/2)) dx = −∫_3 ^( 8) (1/(2(√u) )) du +[ ((√(x^2 −4x+3))/(2(2x−4))) ]_(−1) ^0 = −(1/2)[ 2(√u) ]_3 ^8 + (1/4)[ ((√(x^2 −4x+3))/(x−2)) ]_(−1) ^0 = −(1/2)(4(√2)−2(√3))+(1/4)(−((√3)/2)−0) = (7/8)(√3) −2(√2) _#](Q154357.png)
$$\int_{−\mathrm{1}} ^{\:\mathrm{0}} \:\frac{{x}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}\:}\:{dx} \\ $$$$=\:\int_{−\mathrm{1}} ^{\:\mathrm{0}} \:\frac{\left({x}−\mathrm{2}\right)+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}\:}\:{dx} \\ $$$$=\:\int_{−\mathrm{1}} ^{\:\mathrm{0}} \:\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{x}−\mathrm{4}\right)+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}\:}\:{dx} \\ $$$$=\:\int_{−\mathrm{1}} ^{\:\mathrm{0}} \:\frac{\left(\mathrm{2}{x}−\mathrm{4}\right)+\mathrm{2}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}\:}\:{dx} \\ $$$$=\:\int_{−\mathrm{1}} ^{\:\mathrm{0}} \:\frac{\mathrm{2}{x}−\mathrm{4}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}\:}\:{dx}\:+\int_{−\mathrm{1}} ^{\:\mathrm{0}} \frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}\:}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{let}\:{u}={x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{du}=\left(\mathrm{2}{x}−\mathrm{4}\right)\:{dx} \\ $$$$=\:\int_{\mathrm{8}} ^{\:\mathrm{3}} \frac{\mathrm{1}}{\mathrm{2}\sqrt{{u}}\:}\:{du}\:+\int_{−\mathrm{1}} ^{\:\mathrm{0}} \left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:{dx} \\ $$$$=\:−\int_{\mathrm{3}} ^{\:\mathrm{8}} \:\frac{\mathrm{1}}{\mathrm{2}\sqrt{{u}}\:}\:{du}\:+\left[\:\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}}{\mathrm{2}\left(\mathrm{2}{x}−\mathrm{4}\right)}\:\right]_{−\mathrm{1}} ^{\mathrm{0}} \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{2}}\left[\:\mathrm{2}\sqrt{{u}}\:\right]_{\mathrm{3}} ^{\mathrm{8}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\left[\:\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}}{{x}−\mathrm{2}}\:\right]_{−\mathrm{1}} ^{\mathrm{0}} \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left(−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{0}\right) \\ $$$$=\:\frac{\mathrm{7}}{\mathrm{8}}\sqrt{\mathrm{3}}\:−\mathrm{2}\sqrt{\mathrm{2}}\:_{#} \\ $$
Commented by ZiYangLee last updated on 17/Sep/21
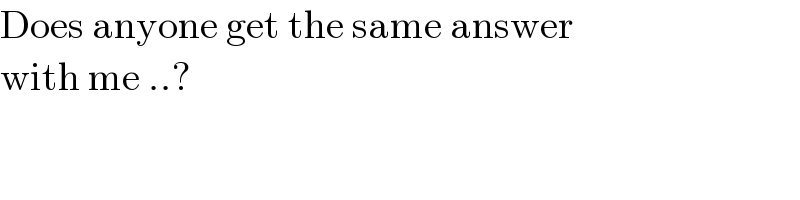
$$\mathrm{Does}\:\mathrm{anyone}\:\mathrm{get}\:\mathrm{the}\:\mathrm{same}\:\mathrm{answer}\: \\ $$$$\mathrm{with}\:\mathrm{me}\:..? \\ $$
Answered by ARUNG_Brandon_MBU last updated on 17/Sep/21
![I=∫_(−1) ^0 ((x−1)/( (√(x^2 −4x+3))))dx =(1/2)∫_(−1) ^0 (((2x−4))/( (√(x^2 −4x+3))))dx+∫_(−1) ^0 (dx/( (√(x^2 −4x+3)))) =(1/2)∫_(−1) ^0 ((d(x^2 −4x+3))/( (√(x^2 −4x+3))))+∫_(−1) ^0 (dx/( (√((x−2)^2 −1)))) =(1/2)∙(2/1)[(√(x^2 −4x+3))]_(−1) ^0 +[argch(x−2)]_(−1) ^0 =(√3)−2(√2)+[ln∣(x−2)+(√((x−2)^2 −1))∣]_(−1) ^0 =(√3)−2(√2)+ln((((√3)−2)/(−1)))=(√3)−2(√2)+ln(2−(√3))](Q154369.png)
$${I}=\int_{−\mathrm{1}} ^{\mathrm{0}} \frac{{x}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}}{dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\mathrm{1}} ^{\mathrm{0}} \frac{\left(\mathrm{2}{x}−\mathrm{4}\right)}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}}{dx}+\int_{−\mathrm{1}} ^{\mathrm{0}} \frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\mathrm{1}} ^{\mathrm{0}} \frac{{d}\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\right)}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}}+\int_{−\mathrm{1}} ^{\mathrm{0}} \frac{{dx}}{\:\sqrt{\left({x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{2}}{\mathrm{1}}\left[\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}}\right]_{−\mathrm{1}} ^{\mathrm{0}} +\left[\mathrm{argch}\left({x}−\mathrm{2}\right)\right]_{−\mathrm{1}} ^{\mathrm{0}} \\ $$$$\:\:=\sqrt{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{2}}+\left[\mathrm{ln}\mid\left({x}−\mathrm{2}\right)+\sqrt{\left({x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{1}}\mid\right]_{−\mathrm{1}} ^{\mathrm{0}} \\ $$$$\:\:=\sqrt{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{ln}\left(\frac{\sqrt{\mathrm{3}}−\mathrm{2}}{−\mathrm{1}}\right)=\sqrt{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{ln}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$
Answered by peter frank last updated on 18/Sep/21
![Q[152270]](Q154428.png)
$$\mathrm{Q}\left[\mathrm{152270}\right] \\ $$
