
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 154268 by liberty last updated on 16/Sep/21

Commented by mr W last updated on 16/Sep/21

$$\mathrm{8}!=\mathrm{40320} \\ $$
Commented by liberty last updated on 17/Sep/21

$${how}? \\ $$
Commented by mr W last updated on 17/Sep/21
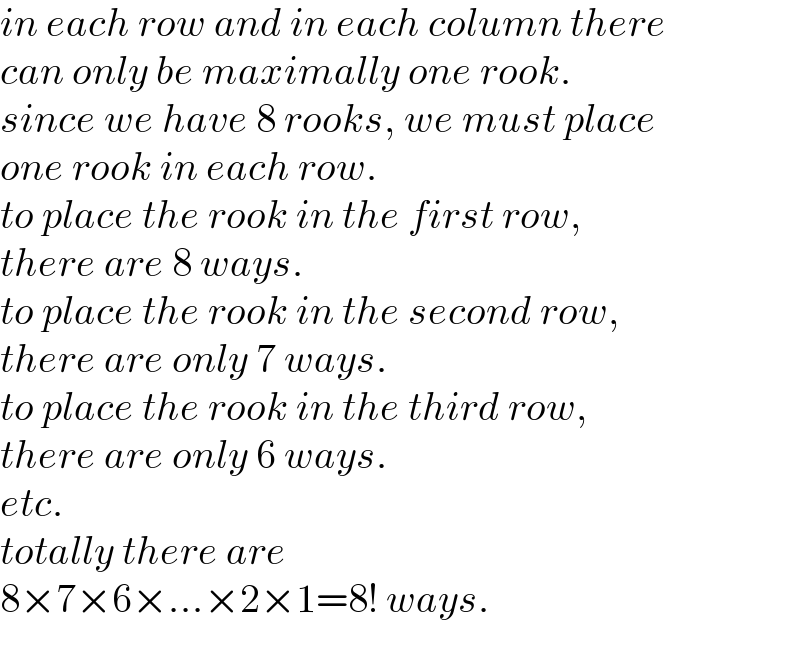
$${in}\:{each}\:{row}\:{and}\:{in}\:{each}\:{column}\:{there} \\ $$$${can}\:{only}\:{be}\:{maximally}\:{one}\:{rook}.\: \\ $$$${since}\:{we}\:{have}\:\mathrm{8}\:{rooks},\:{we}\:{must}\:{place} \\ $$$${one}\:{rook}\:{in}\:{each}\:{row}. \\ $$$${to}\:{place}\:{the}\:{rook}\:{in}\:{the}\:{first}\:{row}, \\ $$$${there}\:{are}\:\mathrm{8}\:{ways}. \\ $$$${to}\:{place}\:{the}\:{rook}\:{in}\:{the}\:{second}\:{row}, \\ $$$${there}\:{are}\:{only}\:\mathrm{7}\:{ways}. \\ $$$${to}\:{place}\:{the}\:{rook}\:{in}\:{the}\:{third}\:{row}, \\ $$$${there}\:{are}\:{only}\:\mathrm{6}\:{ways}. \\ $$$${etc}. \\ $$$${totally}\:{there}\:{are} \\ $$$$\mathrm{8}×\mathrm{7}×\mathrm{6}×...×\mathrm{2}×\mathrm{1}=\mathrm{8}!\:{ways}. \\ $$
