
Question Number 154235 by mnjuly1970 last updated on 15/Sep/21
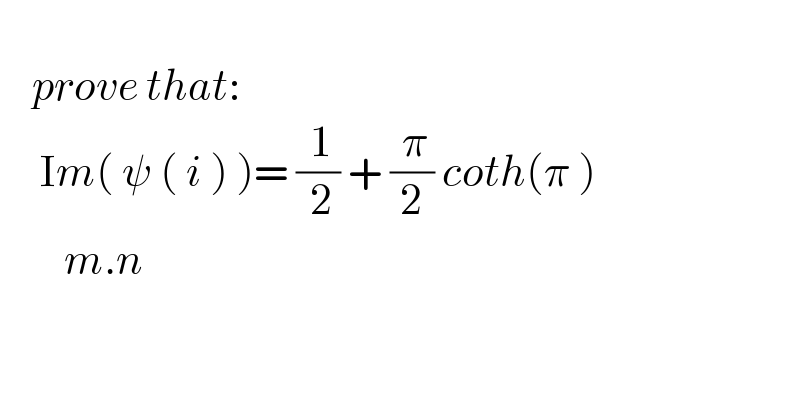
$$ \\ $$$$\:\:\:\:{prove}\:{that}: \\ $$$$\:\:\:\:\:\mathrm{I}{m}\left(\:\psi\:\left(\:{i}\:\right)\:\right)=\:\frac{\:\mathrm{1}}{\:\mathrm{2}}\:+\:\frac{\:\pi}{\mathrm{2}}\:{coth}\left(\pi\:\right) \\ $$$$\:\:\:\:\:\:\:\:{m}.{n} \\ $$
Answered by mindispower last updated on 16/Sep/21
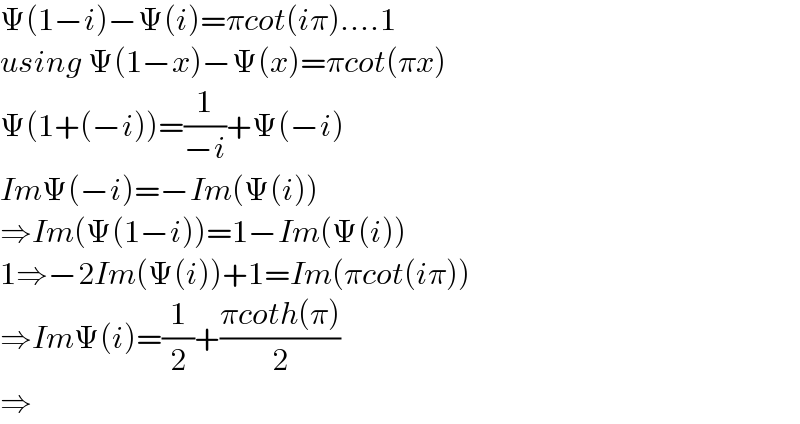
$$\Psi\left(\mathrm{1}−{i}\right)−\Psi\left({i}\right)=\pi{cot}\left({i}\pi\right)....\mathrm{1} \\ $$$${using}\:\Psi\left(\mathrm{1}−{x}\right)−\Psi\left({x}\right)=\pi{cot}\left(\pi{x}\right) \\ $$$$\Psi\left(\mathrm{1}+\left(−{i}\right)\right)=\frac{\mathrm{1}}{−{i}}+\Psi\left(−{i}\right) \\ $$$${Im}\Psi\left(−{i}\right)=−{Im}\left(\Psi\left({i}\right)\right) \\ $$$$\Rightarrow{Im}\left(\Psi\left(\mathrm{1}−{i}\right)\right)=\mathrm{1}−{Im}\left(\Psi\left({i}\right)\right) \\ $$$$\mathrm{1}\Rightarrow−\mathrm{2}{Im}\left(\Psi\left({i}\right)\right)+\mathrm{1}={Im}\left(\pi{cot}\left({i}\pi\right)\right) \\ $$$$\Rightarrow{Im}\Psi\left({i}\right)=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi{coth}\left(\pi\right)}{\mathrm{2}} \\ $$$$\Rightarrow \\ $$
Commented by mnjuly1970 last updated on 16/Sep/21
$$\:{thanks}\:{alot}...{mr}\:{power} \\ $$
Commented by mindispower last updated on 16/Sep/21

$${pleasur} \\ $$
