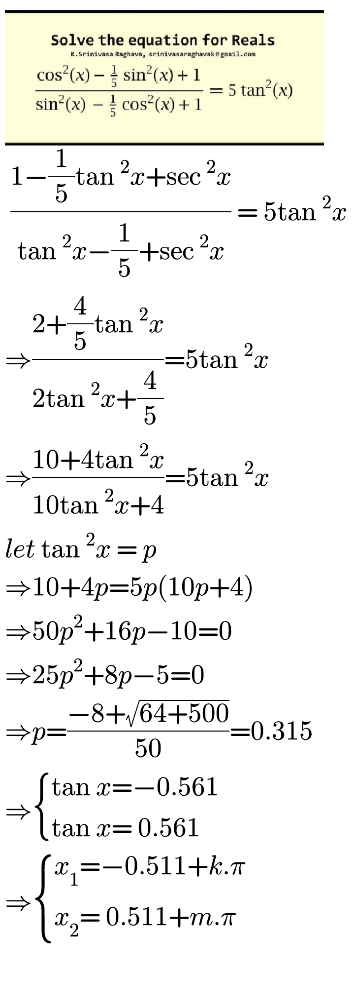Question Number 154216 by EDWIN88 last updated on 15/Sep/21

$${Solve}\:{the}\:{equation}\:{for}\:{reals}\: \\ $$$$\:\frac{\mathrm{cos}\:^{\mathrm{2}} {x}−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} {x}−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{1}}\:=\:\mathrm{5tan}\:^{\mathrm{2}} {x}\: \\ $$
Answered by MJS_new last updated on 15/Sep/21
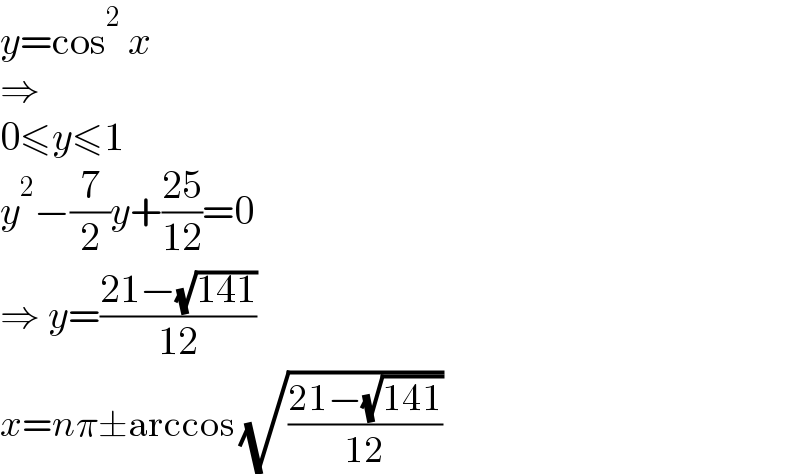
$${y}=\mathrm{cos}^{\mathrm{2}} \:{x} \\ $$$$\Rightarrow \\ $$$$\mathrm{0}\leqslant{y}\leqslant\mathrm{1} \\ $$$${y}^{\mathrm{2}} −\frac{\mathrm{7}}{\mathrm{2}}{y}+\frac{\mathrm{25}}{\mathrm{12}}=\mathrm{0} \\ $$$$\Rightarrow\:{y}=\frac{\mathrm{21}−\sqrt{\mathrm{141}}}{\mathrm{12}} \\ $$$${x}={n}\pi\pm\mathrm{arccos}\:\sqrt{\frac{\mathrm{21}−\sqrt{\mathrm{141}}}{\mathrm{12}}} \\ $$
Answered by benhamimed last updated on 15/Sep/21

$$\frac{−\mathrm{sin}\:^{\mathrm{2}} {x}+\frac{\mathrm{1}}{\mathrm{5}}\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{1}+\mathrm{1}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}+\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} {x}−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{1}}=\mathrm{5}\frac{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}}{\mathrm{cos}\:\:^{\mathrm{2}} {x}} \\ $$$$−\mathrm{1}+\frac{\frac{\mathrm{14}}{\mathrm{5}}}{\mathrm{2sin}\:^{\mathrm{2}} {x}+\frac{\mathrm{4}}{\mathrm{5}}\mathrm{cos}\:^{\mathrm{2}} {x}}=\frac{\mathrm{5}}{\mathrm{cos}\:^{\mathrm{2}} {x}}−\mathrm{5} \\ $$$$\frac{\mathrm{14}}{\mathrm{5}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)+\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}\right)}=\frac{\mathrm{5}}{\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}}−\mathrm{4} \\ $$$$\frac{\mathrm{14}}{\mathrm{7}−\mathrm{3cos}\:\mathrm{2}{x}}=\frac{\mathrm{10}−\mathrm{4}−\mathrm{4cos}\:\mathrm{2}{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}} \\ $$$$\left(\mathrm{6}−\mathrm{4cos}\:\mathrm{2}{x}\right)\left(\mathrm{7}−\mathrm{3cos}\:\mathrm{2}{x}\right)=\mathrm{14}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}\right) \\ $$$$\mathrm{12cos}\:^{\mathrm{2}} \left(\mathrm{2}{x}\right)−\mathrm{60cos}\:\left(\mathrm{2}{x}\right)+\mathrm{28}=\mathrm{0} \\ $$$$\mathrm{3cos}\:^{\mathrm{2}} \left(\mathrm{2}{x}\right)−\mathrm{15cos}\:\left(\mathrm{2}{x}\right)+\mathrm{7}=\mathrm{0} \\ $$$$\Delta=\mathrm{141} \\ $$$$\mathrm{cos}\:\left(\mathrm{2}{x}\right)=\frac{\mathrm{15}−\sqrt{\mathrm{141}}}{\mathrm{6}}\:\: \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{15}−\sqrt{\mathrm{141}}}{\mathrm{6}}\right) \\ $$
Answered by liberty last updated on 16/Sep/21