
Question Number 154195 by rexford last updated on 15/Sep/21

$$\int\frac{{x}+{sinx}}{\mathrm{1}+{cosx}}{dx}\:\:\:\: \\ $$$${please},{help}\:{me} \\ $$
Answered by qaz last updated on 15/Sep/21
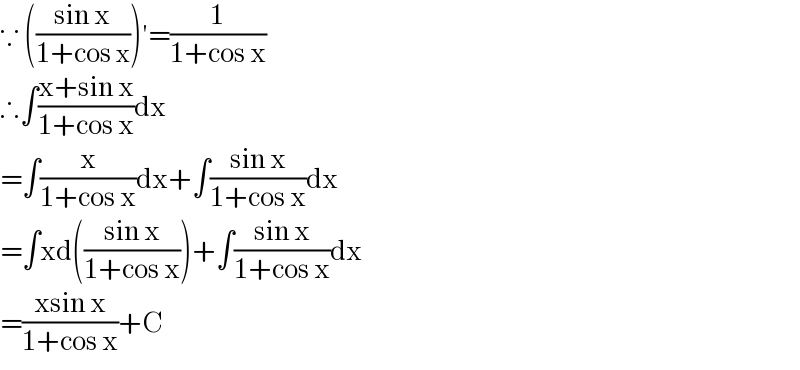
$$\because\:\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}\right)'=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}} \\ $$$$\therefore\int\frac{\mathrm{x}+\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}\mathrm{dx} \\ $$$$=\int\frac{\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}\mathrm{dx}+\int\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}\mathrm{dx} \\ $$$$=\int\mathrm{xd}\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}\right)+\int\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}\mathrm{dx} \\ $$$$=\frac{\mathrm{xsin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}+\mathrm{C} \\ $$
Commented by qaz last updated on 15/Sep/21
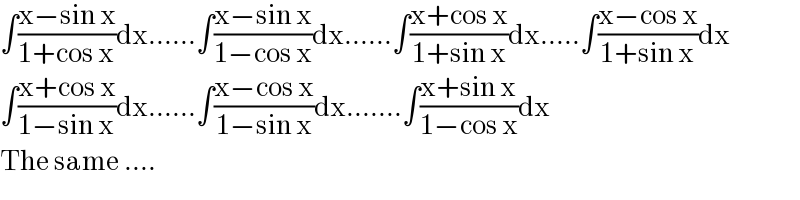
$$\int\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}\mathrm{dx}......\int\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{1}−\mathrm{cos}\:\mathrm{x}}\mathrm{dx}......\int\frac{\mathrm{x}+\mathrm{cos}\:\mathrm{x}}{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}\mathrm{dx}.....\int\frac{\mathrm{x}−\mathrm{cos}\:\mathrm{x}}{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}\mathrm{dx} \\ $$$$\int\frac{\mathrm{x}+\mathrm{cos}\:\mathrm{x}}{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}\mathrm{dx}......\int\frac{\mathrm{x}−\mathrm{cos}\:\mathrm{x}}{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}\mathrm{dx}.......\int\frac{\mathrm{x}+\mathrm{sin}\:\mathrm{x}}{\mathrm{1}−\mathrm{cos}\:\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{The}\:\mathrm{same}\:.... \\ $$
Answered by puissant last updated on 15/Sep/21
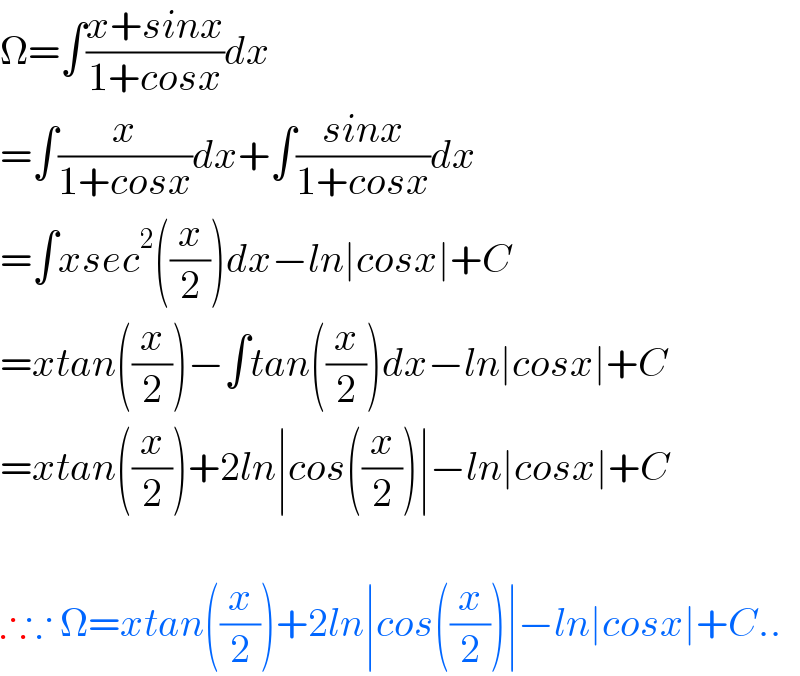
$$\Omega=\int\frac{{x}+{sinx}}{\mathrm{1}+{cosx}}{dx} \\ $$$$=\int\frac{{x}}{\mathrm{1}+{cosx}}{dx}+\int\frac{{sinx}}{\mathrm{1}+{cosx}}{dx} \\ $$$$=\int{xsec}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right){dx}−{ln}\mid{cosx}\mid+{C} \\ $$$$={xtan}\left(\frac{{x}}{\mathrm{2}}\right)−\int{tan}\left(\frac{{x}}{\mathrm{2}}\right){dx}−{ln}\mid{cosx}\mid+{C} \\ $$$$={xtan}\left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{2}{ln}\mid{cos}\left(\frac{{x}}{\mathrm{2}}\right)\mid−{ln}\mid{cosx}\mid+{C} \\ $$$$ \\ $$$$\therefore\because\:\Omega={xtan}\left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{2}{ln}\mid{cos}\left(\frac{{x}}{\mathrm{2}}\right)\mid−{ln}\mid{cosx}\mid+{C}.. \\ $$
Answered by maged last updated on 15/Sep/21

$${I}=\int\frac{{x}}{\mathrm{1}+\mathrm{cos}{x}}.\frac{\mathrm{1}−\mathrm{cos}{x}}{\mathrm{1}−\mathrm{cos}{x}}{dx}+\int\frac{\mathrm{sin}{x}}{\mathrm{1}+\mathrm{cos}{x}}.\frac{\mathrm{1}−\mathrm{cos}{x}}{\mathrm{1}−\mathrm{cos}{x}}{dx} \\ $$$$=\int\frac{{x}\left(\mathrm{1}−\mathrm{cos}{x}\right)}{\mathrm{sin}^{\mathrm{2}} {x}}{dx}+\int\frac{\mathrm{1}}{\mathrm{sin}{x}}{dx} \\ $$$${I}=\int{x}\mathrm{cosec}^{\mathrm{2}} {xdx}−\int{x}\mathrm{cot}{x}\mathrm{cosec}{xdx}+\int\mathrm{cosec}{xdx} \\ $$$${u}={x}\rightarrow{du}={dx} \\ $$$${dv}=\mathrm{cosec}^{\mathrm{2}} {xdx}\rightarrow{v}=−\mathrm{cot}{x}\: \\ $$$$−− \\ $$$${u}={x}\rightarrow{du}={dx} \\ $$$${dv}=−\mathrm{cot}{x}\mathrm{cosec}{xdx}\rightarrow{v}=\mathrm{cosec}{x} \\ $$$$−− \\ $$$${I}=−{x}\mathrm{cot}{x}+{x}\mathrm{cosec}{x}+\int\mathrm{cot}{xdx}−\int\mathrm{cosec}{xdx}+\int\mathrm{cosec}{xdx} \\ $$$$={x}\mathrm{cosec}{x}−{x}\mathrm{cot}{x}−\mathrm{ln}\left(\mathrm{sin}{x}\right)+{C} \\ $$
