
Question Number 154020 by mnjuly1970 last updated on 13/Sep/21
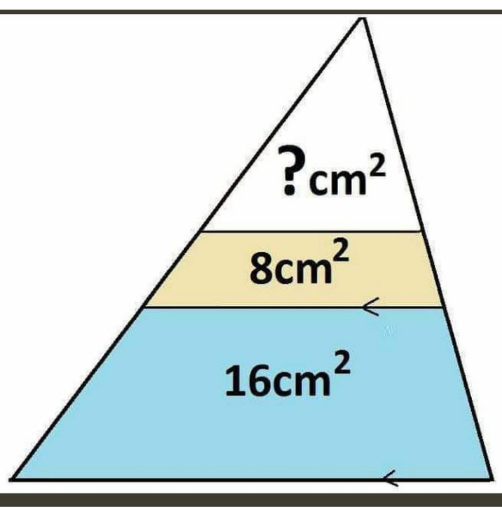
Commented by mr W last updated on 13/Sep/21
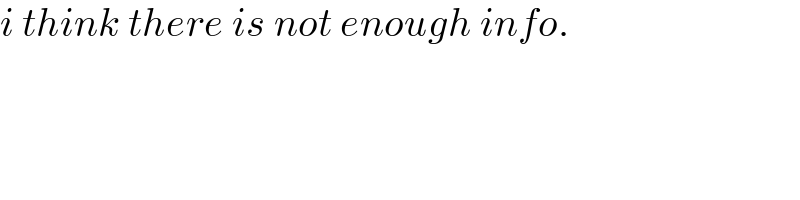
$${i}\:{think}\:{there}\:{is}\:{not}\:{enough}\:{info}. \\ $$
Commented by mr W last updated on 13/Sep/21
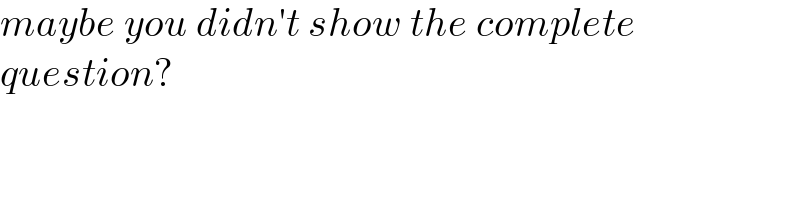
$${maybe}\:{you}\:{didn}'{t}\:{show}\:{the}\:{complete} \\ $$$${question}? \\ $$
Commented by talminator2856791 last updated on 13/Sep/21
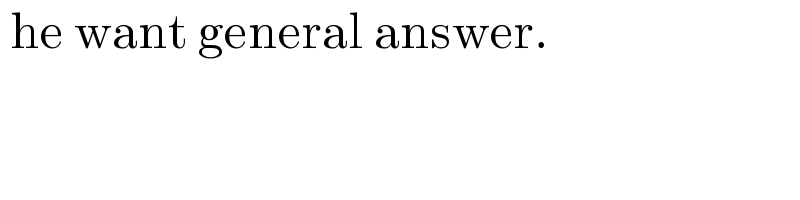
$$\:\mathrm{he}\:\mathrm{want}\:\mathrm{general}\:\mathrm{answer}. \\ $$
Commented by mr W last updated on 13/Sep/21

$${if}\:{the}\:{condition}\:{is}\:{not}\:{given},\:{there} \\ $$$${is}\:{no}\:{answer},\:{also}\:{no}\:{general}\:{answer}. \\ $$$${x}\:{can}\:{be}\:{any}\:{position}\:{value}\:{with} \\ $$$${given}\:{information}. \\ $$
Commented by talminator2856791 last updated on 13/Sep/21

$$\:\mathrm{there}\:\mathrm{is}\:\mathrm{a}\:\mathrm{condition}. \\ $$$$\:\mathrm{the}\:\mathrm{given}\:\mathrm{information}\:\mathrm{is}\:\mathrm{enough} \\ $$$$\:\mathrm{for}\:\mathrm{some}\:\mathrm{general}\:\mathrm{form}. \\ $$$$\:\mathrm{just}\:\mathrm{give}\:\mathrm{the}\:\mathrm{angles}\:\mathrm{and}\:\mathrm{sides}\:\mathrm{variables}\: \\ $$$$\:\mathrm{and}\:\mathrm{solve}\:\mathrm{like}\:\mathrm{that}. \\ $$$$\:\:\mathrm{i}.\mathrm{e}\:\mathrm{applying}\:\mathrm{heron}'\mathrm{s}\:\mathrm{formula} \\ $$$$\:\:\mathrm{and}\:\mathrm{then}\:\mathrm{making}\:{x}\:\mathrm{the}\:\mathrm{subject} \\ $$$$\:\:\mathrm{of}\:\mathrm{the}\:\mathrm{formula}. \\ $$
Commented by mr W last updated on 13/Sep/21

$${i}\:{don}'{t}\:{need}\:{any}\:{formula},\:{i}\:{only}\:{need} \\ $$$${the}\:{logic}\:{in}\:{order}\:{to}\:{see}\:{that}\:{the}\:{area} \\ $$$$?\:{can}\:{not}\:{be}\:{determined}\:{with}\:{the} \\ $$$${conditions}\:{given}\:{in}\:{the}\:{question}. \\ $$
Commented by mr W last updated on 13/Sep/21
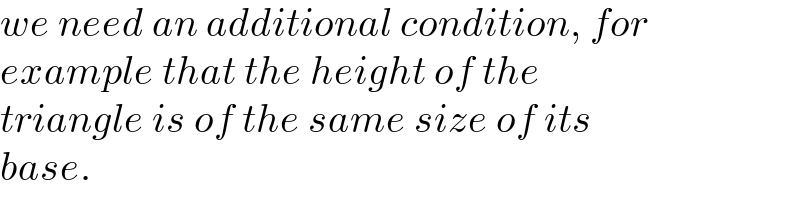
$${we}\:{need}\:{an}\:{additional}\:{condition},\:{for} \\ $$$${example}\:{that}\:{the}\:{height}\:{of}\:{the} \\ $$$${triangle}\:{is}\:{of}\:{the}\:{same}\:{size}\:{of}\:{its} \\ $$$${base}. \\ $$
Answered by lyubita last updated on 13/Sep/21

$$\mathrm{1}\:{cm}^{\mathrm{2}} \\ $$
Answered by lyubita last updated on 13/Sep/21
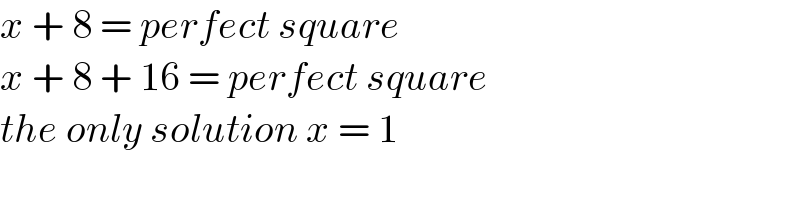
$${x}\:+\:\mathrm{8}\:=\:{perfect}\:{square} \\ $$$${x}\:+\:\mathrm{8}\:+\:\mathrm{16}\:=\:{perfect}\:{square} \\ $$$${the}\:{only}\:{solution}\:{x}\:=\:\mathrm{1} \\ $$
Commented by mr W last updated on 13/Sep/21

$${who}\:{said}\:{it}\:{should}\:{be}\:{perfect}\:{square}. \\ $$$${i}\:{can}\:{also}\:{say},\:{they}\:{are}: \\ $$$$\mathrm{16}=\mathrm{2}^{\mathrm{4}} ,\:\mathrm{8}=\mathrm{2}^{\mathrm{3}} ,\:{x}=\mathrm{2}^{\mathrm{2}} =\mathrm{4}. \\ $$$$ \\ $$$${if}\:{the}\:{rule}\:{is}\:{not}\:{defined},\:{x}\:{can}\:{be} \\ $$$${any}\:{positive}\:{value}\:{you}\:{want}\:{it}\:{to}\:{have}. \\ $$$$ \\ $$$${i}\:{think}\:{it}\:{makes}\:{no}\:{sense}\:{trying}\:{to} \\ $$$${solve}\:{a}\:{question}\:{which}\:{is}\:{not}\:{clear} \\ $$
Commented by Rasheed.Sindhi last updated on 13/Sep/21
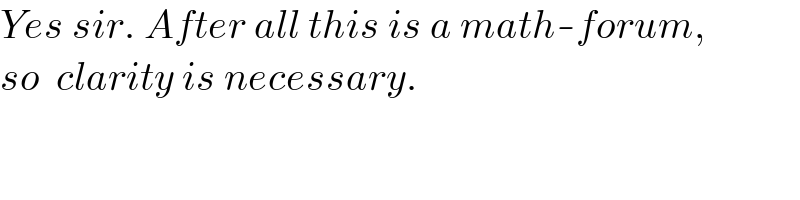
$${Yes}\:{sir}.\:{After}\:{all}\:{this}\:{is}\:{a}\:{math}-{forum}, \\ $$$${so}\:\:{clarity}\:{is}\:{necessary}. \\ $$
