
Question Number 154012 by mathdanisur last updated on 13/Sep/21

$$\mathrm{Determine}\:\mathrm{all}\:\mathrm{the}\:\mathrm{perfect}\:\mathrm{squares}\:\mathrm{on} \\ $$$$\mathrm{form}\:\:\boldsymbol{\mathrm{p}}^{\boldsymbol{\mathrm{n}}} \:+\:\mathrm{1}\:\:\mathrm{where}\:\:\boldsymbol{\mathrm{p}}\:\:\mathrm{is}\:\mathrm{a}\:\mathrm{prime}\:\mathrm{number} \\ $$$$\mathrm{and}\:\:\boldsymbol{\mathrm{n}}\:\:\mathrm{a}\:\mathrm{positive}\:\mathrm{integer}. \\ $$
Commented by Rasheed.Sindhi last updated on 13/Sep/21

$$\mathrm{For}\:\mathrm{some}\:\mathrm{cases} \\ $$$$\boldsymbol{\mathrm{p}}^{\boldsymbol{\mathrm{n}}} \:+\:\mathrm{1}=\mathrm{q}^{\mathrm{2}} \Rightarrow\mathrm{q}^{\mathrm{2}} −\mathrm{1}=\mathrm{p}^{\mathrm{n}} \\ $$$$\left(\mathrm{q}−\mathrm{1}\right)\left(\mathrm{q}+\mathrm{1}\right)=\mathrm{p}^{\mathrm{n}} \\ $$$$\mathrm{n}=\mathrm{1}:\:\left(\mathrm{q}−\mathrm{1}\right)\left(\mathrm{q}+\mathrm{1}\right)=\mathrm{p} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{q}−\mathrm{1}=\mathrm{1}\wedge\:\mathrm{q}+\mathrm{1}=\mathrm{p} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{q}=\mathrm{2}\:\wedge\:\mathrm{p}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{q}^{\mathrm{2}} =\mathrm{4} \\ $$$$\mathrm{n}=\mathrm{2}:\left(\mathrm{q}−\mathrm{1}\right)\left(\mathrm{q}+\mathrm{1}\right)=\mathrm{p}^{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{case1}:\:\mathrm{q}−\mathrm{1}=\mathrm{1}\wedge\:\mathrm{q}+\mathrm{1}=\mathrm{p}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{q}=\mathrm{2}\:\:\wedge\:\mathrm{p}^{\mathrm{2}} =\mathrm{3}\:\left(\mathrm{false}\right) \\ $$$$\:\:\:\:\mathrm{case2}:\:\mathrm{q}−\mathrm{1}=\mathrm{q}+\mathrm{1}=\mathrm{p}\left(\mathrm{false}\right) \\ $$$$\:\:\:\:\mathrm{For}\:\mathrm{n}=\mathrm{2}\:\mathrm{no}\:\mathrm{p} \\ $$$$\mathrm{n}=\mathrm{3}:\mathrm{q}^{\mathrm{2}} −\mathrm{1}=\mathrm{p}^{\mathrm{3}} \\ $$$$\:\:\:\:\mathrm{p}^{\mathrm{3}} +\mathrm{1}=\mathrm{q}^{\mathrm{2}} \\ $$$$\:\:\:\left(\mathrm{p}+\mathrm{1}\right)\left(\mathrm{p}^{\mathrm{2}} −\mathrm{p}+\mathrm{1}\right)=\mathrm{q}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{p}+\mathrm{1}=\mathrm{p}^{\mathrm{2}} −\mathrm{p}+\mathrm{1} \\ $$$$\:\:\:\:\:\mathrm{p}^{\mathrm{2}} −\mathrm{2p}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{p}\left(\mathrm{p}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\:\:\:\:\mathrm{p}=\mathrm{0}\left(\mathrm{false}\right)\:\vee\:\mathrm{p}=\mathrm{2}\:\left(\mathrm{true}\right) \\ $$$$\:\:\:\:\mathrm{p}=\mathrm{2}\Rightarrow\mathrm{q}^{\mathrm{2}} =\mathrm{p}^{\mathrm{3}} +\mathrm{1}=\mathrm{2}^{\mathrm{3}} +\mathrm{1}=\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{q}^{\mathrm{2}} =\mathrm{9} \\ $$
Commented by mathdanisur last updated on 13/Sep/21
$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{Ser},\:\mathrm{thank}\:\mathrm{you} \\ $$
Answered by Rasheed.Sindhi last updated on 14/Sep/21

$$\boldsymbol{\mathrm{p}}^{\boldsymbol{\mathrm{n}}} \:+\:\mathrm{1}=\mathrm{q}^{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{p}}^{\boldsymbol{\mathrm{n}}} \:=\left(\mathrm{q}−\mathrm{1}\right)\left(\mathrm{q}+\mathrm{1}\right) \\ $$$$\mathrm{q}−\mathrm{1}=\mathrm{p}^{\mathrm{m}} \Rightarrow\mathrm{q}+\mathrm{1}=\mathrm{p}^{\mathrm{n}−\mathrm{m}} \\ $$$$\mathrm{p}^{\mathrm{n}−\mathrm{m}} −\mathrm{p}^{\mathrm{m}} =\left(\mathrm{q}+\mathrm{1}\right)−\left(\mathrm{q}−\mathrm{1}\right)=\mathrm{2} \\ $$$$\mathrm{p}^{\mathrm{n}−\mathrm{m}} −\mathrm{p}^{\mathrm{m}} =\mathrm{2} \\ $$$$\left(\mathcal{T}{wo}\:{powers}\:{of}\:{a}\:{prime}\:{having}\:\right. \\ $$$$\left.{difference}\:\mathrm{2}\right) \\ $$$$\:\:\:\:\mathrm{2}^{\mathrm{2}} −\mathrm{2}^{\mathrm{1}} =\mathrm{2}\Rightarrow\mathrm{q}−\mathrm{1}=\mathrm{2}\:\wedge\:\mathrm{q}+\mathrm{1}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{q}^{\mathrm{2}} −\mathrm{1}=\mathrm{8}\Rightarrow\mathrm{q}^{\mathrm{2}} =\mathrm{9} \\ $$$$\left({Only}\:{these}\:{two}\:{powers}\:{of}\:\mathrm{2}\:{have}\:\right. \\ $$$$\left.{difference}\:\mathrm{2}\right)^{\bigstar} \\ $$$$\:\:\:\:\mathrm{3}^{\mathrm{1}} −\mathrm{3}^{\mathrm{0}} =\mathrm{2}\Rightarrow\mathrm{q}−\mathrm{1}=\mathrm{3}^{\mathrm{0}} \:\wedge\:\mathrm{q}+\mathrm{1}=\mathrm{3}^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{q}^{\mathrm{2}} −\mathrm{1}=\mathrm{3}\Rightarrow\mathrm{q}^{\mathrm{2}} =\mathrm{4} \\ $$$$\left({Only}\:{these}\:{two}\:{powers}\:{of}\:\mathrm{3}\:{have}\:\right. \\ $$$$\left.{difference}\:\mathrm{2}\right)^{\bigstar\bigstar} \\ $$$$\:\:\mathrm{p}>\mathrm{3}:\mathrm{p}^{\mathrm{m}} −\mathrm{p}^{\mathrm{n}} >\mathrm{2}\:{for}\:{any}\:{m},{n} \\ $$
Commented by Rasheed.Sindhi last updated on 14/Sep/21
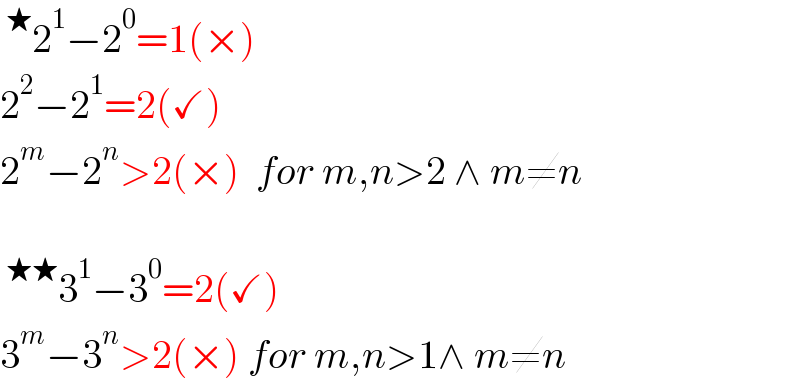
$$\:^{\bigstar} \mathrm{2}^{\mathrm{1}} −\mathrm{2}^{\mathrm{0}} =\mathrm{1}\left(×\right) \\ $$$$\mathrm{2}^{\mathrm{2}} −\mathrm{2}^{\mathrm{1}} =\mathrm{2}\left(\checkmark\right) \\ $$$$\mathrm{2}^{{m}} −\mathrm{2}^{{n}} >\mathrm{2}\left(×\right)\:\:{for}\:{m},{n}>\mathrm{2}\:\wedge\:{m}\neq{n} \\ $$$$ \\ $$$$\:^{\bigstar\bigstar} \mathrm{3}^{\mathrm{1}} −\mathrm{3}^{\mathrm{0}} =\mathrm{2}\left(\checkmark\right) \\ $$$$\mathrm{3}^{{m}} −\mathrm{3}^{{n}} >\mathrm{2}\left(×\right)\:{for}\:{m},{n}>\mathrm{1}\wedge\:{m}\neq{n} \\ $$
Commented by mathdanisur last updated on 14/Sep/21
$$\mathrm{very}\:\mathrm{nice}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{thanks} \\ $$
