
Question Number 153963 by ZiYangLee last updated on 12/Sep/21
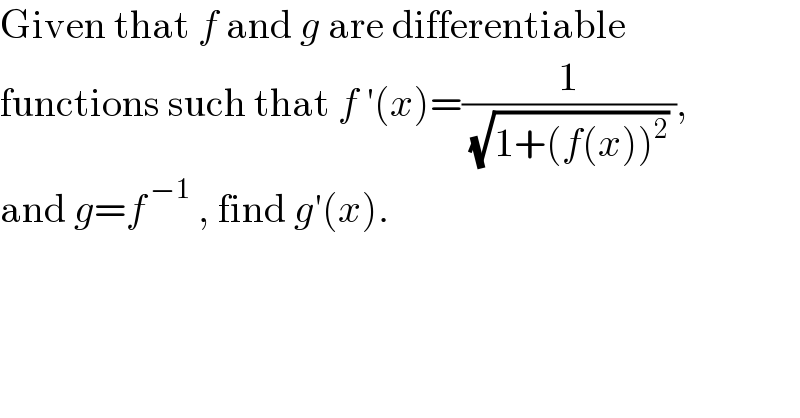
$$\mathrm{Given}\:\mathrm{that}\:{f}\:\mathrm{and}\:{g}\:\mathrm{are}\:\mathrm{differentiable} \\ $$$$\mathrm{functions}\:\mathrm{such}\:\mathrm{that}\:{f}\:'\left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\left({f}\left({x}\right)\right)^{\mathrm{2}} }\:}, \\ $$$$\mathrm{and}\:{g}={f}^{\:−\mathrm{1}} \:,\:\mathrm{find}\:{g}'\left({x}\right). \\ $$
Answered by mr W last updated on 12/Sep/21
![y=f(x) y′=(1/( (√(1+y^2 )))) (√(1+y^2 ))dy=dx (1/2)[ln (y+(√(1+y^2 )))+y(√(1+y^2 ))]+C=x ⇒g(x)=f^(−1) (x)=(1/2)[ln (x+(√(1+x^2 )))+x(√(1+x^2 ))]+C g′(x)=(1/2)[((1+(x/( (√(1+x^2 )))))/(x+(√(1+x^2 ))))+(√(1+x^2 ))+(x^2 /( (√(1+x^2 ))))] =(1/2)[((x+(√(1+x^2 )))/(x+(√(1+x^2 ))))+1+2x^2 ](1/( (√(1+x^2 )))) =(√(1+x^2 ))](Q153967.png)
$${y}={f}\left({x}\right) \\ $$$${y}'=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }} \\ $$$$\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }{dy}={dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\:\left({y}+\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }\right)+{y}\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }\right]+{C}={x} \\ $$$$\Rightarrow{g}\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)+{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right]+{C} \\ $$$${g}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}+\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}}{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }+\frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}+\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} \right]\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$$=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$
Commented by ZiYangLee last updated on 12/Sep/21
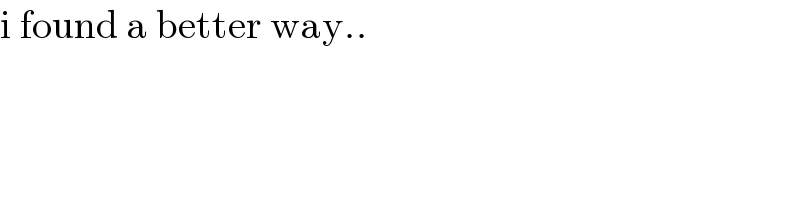
$$\mathrm{i}\:\mathrm{found}\:\mathrm{a}\:\mathrm{better}\:\mathrm{way}.. \\ $$
Commented by mr W last updated on 12/Sep/21
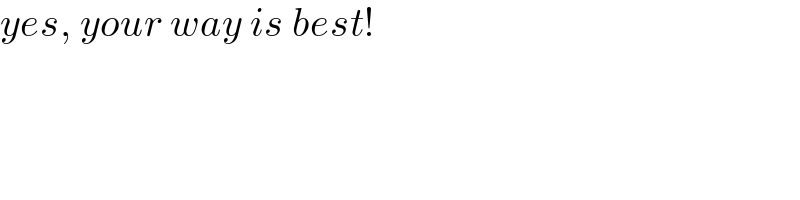
$${yes},\:{your}\:{way}\:{is}\:{best}! \\ $$
Answered by ZiYangLee last updated on 12/Sep/21
![let g(x)=f^( −1) (x)=y f(y)=x f ′(x) (dy/dx) =1 (1/( (√(1+[f(y)]^2 )) )) (dy/dx) =1 (dy/dx)= (√(1+[f(y)]^2 )) g ′(x)= (√(1+[f(y)]^2 )) g ′(x)= (√(1+x^2 )) _#](Q153991.png)
$${let}\:{g}\left({x}\right)={f}^{\:−\mathrm{1}} \left({x}\right)={y} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\left({y}\right)={x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\:'\left({x}\right)\:\frac{{dy}}{{dx}}\:=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\left[{f}\left({y}\right)\right]^{\mathrm{2}} }\:}\:\frac{{dy}}{{dx}}\:=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{dy}}{{dx}}=\:\sqrt{\mathrm{1}+\left[{f}\left({y}\right)\right]^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{g}\:'\left({x}\right)=\:\sqrt{\mathrm{1}+\left[{f}\left({y}\right)\right]^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{g}\:'\left({x}\right)=\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:_{#} \\ $$
