
Question Number 153956 by liberty last updated on 12/Sep/21
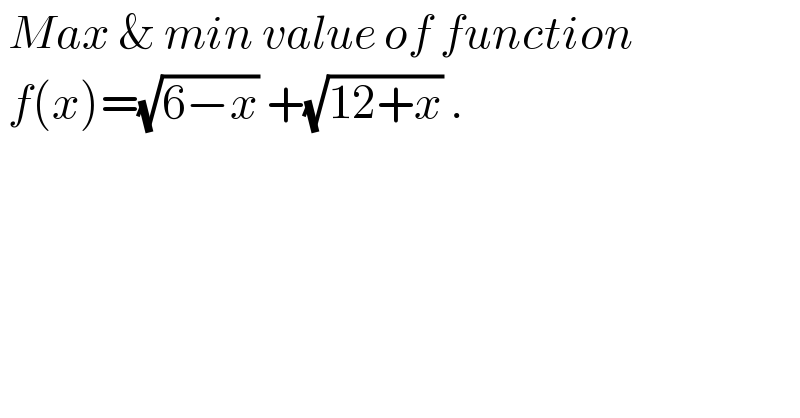
$$\:{Max}\:\&\:{min}\:{value}\:{of}\:{function} \\ $$ $$\:{f}\left({x}\right)=\sqrt{\mathrm{6}−{x}}\:+\sqrt{\mathrm{12}+{x}}\:. \\ $$
Answered by EDWIN88 last updated on 12/Sep/21
![domain of f(x) = [−12,6 ] by Chaucy −Schward inequality 2[(6−x)+(12+x) ]≥ ((√(6−x))+(√(12+x)) )^2 2×18 ≥ [ (√(6−x)) +(√(12+x)) ]^2 ⇒(√(18)) ≤ (√(6−x)) +(√(12+x)) ≤ (√(36)) ⇒3(√2) ≤ (√(6−x)) +(√(12+x)) ≤ 6 { ((min=3(√2))),((max=6)) :}](Q153974.png)
$$\:{domain}\:{of}\:{f}\left({x}\right)\:=\:\left[−\mathrm{12},\mathrm{6}\:\right] \\ $$ $${by}\:{Chaucy}\:−{Schward}\:{inequality} \\ $$ $$\mathrm{2}\left[\left(\mathrm{6}−{x}\right)+\left(\mathrm{12}+{x}\right)\:\right]\geqslant\:\left(\sqrt{\mathrm{6}−{x}}+\sqrt{\mathrm{12}+{x}}\:\right)^{\mathrm{2}} \\ $$ $$\mathrm{2}×\mathrm{18}\:\geqslant\:\left[\:\sqrt{\mathrm{6}−{x}}\:+\sqrt{\mathrm{12}+{x}}\:\right]^{\mathrm{2}} \\ $$ $$\Rightarrow\sqrt{\mathrm{18}}\:\leqslant\:\sqrt{\mathrm{6}−{x}}\:+\sqrt{\mathrm{12}+{x}}\:\leqslant\:\sqrt{\mathrm{36}} \\ $$ $$\Rightarrow\mathrm{3}\sqrt{\mathrm{2}}\:\leqslant\:\sqrt{\mathrm{6}−{x}}\:+\sqrt{\mathrm{12}+{x}}\:\leqslant\:\mathrm{6} \\ $$ $$\:\begin{cases}{{min}=\mathrm{3}\sqrt{\mathrm{2}}}\\{{max}=\mathrm{6}}\end{cases} \\ $$
Commented byliberty last updated on 13/Sep/21

$${yes}\:{correct} \\ $$
Answered by ajfour last updated on 15/Sep/21
![let x−3=t f(t)=(√(9−t))+(√(9+t)) ⇒ t∈[−9,9] f^( 2) (t)=18+2(√(81−t^2 )) clearly f_(min) =3(√2), f_(max) =6](Q154199.png)
$${let}\:\:{x}−\mathrm{3}={t} \\ $$ $${f}\left({t}\right)=\sqrt{\mathrm{9}−{t}}+\sqrt{\mathrm{9}+{t}} \\ $$ $$\Rightarrow\:\:\:\:\:{t}\in\left[−\mathrm{9},\mathrm{9}\right] \\ $$ $${f}^{\:\mathrm{2}} \left({t}\right)=\mathrm{18}+\mathrm{2}\sqrt{\mathrm{81}−{t}^{\mathrm{2}} } \\ $$ $${clearly}\:{f}_{{min}} =\mathrm{3}\sqrt{\mathrm{2}},\:\:{f}_{{max}} =\mathrm{6} \\ $$
